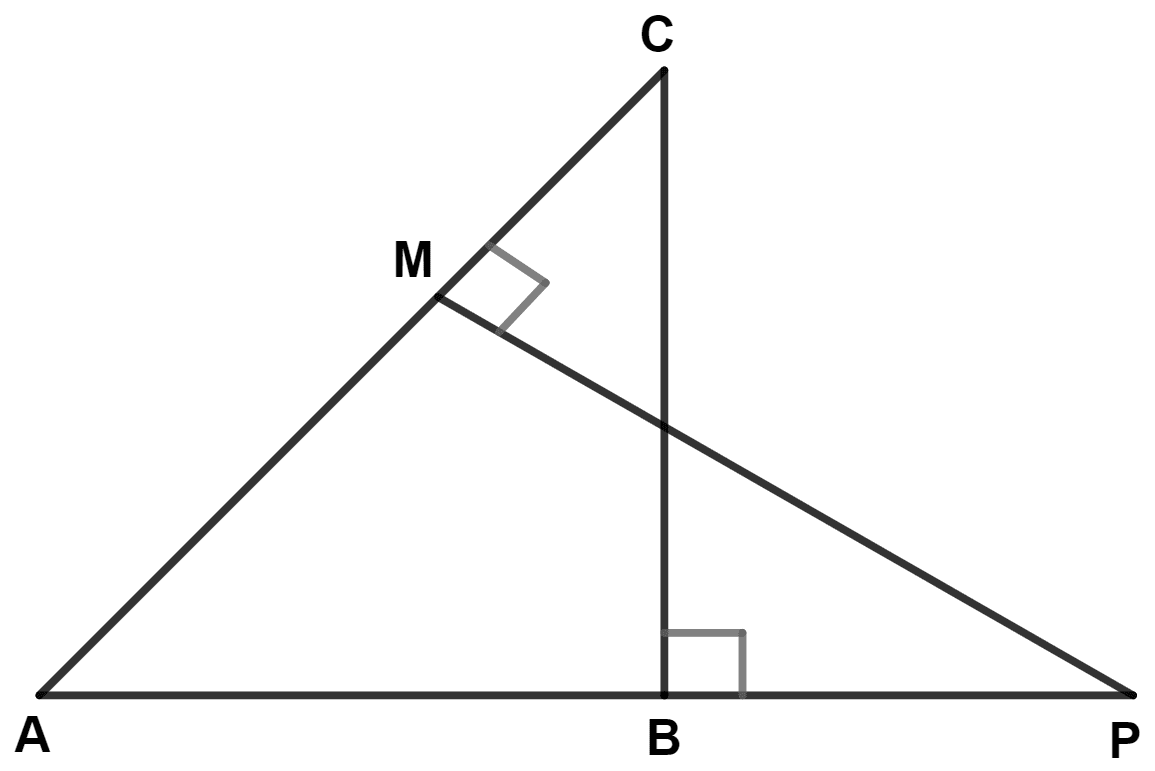
The given figure shows two triangles ABC and AMP, right angled at points B and M respectively.

(i) Prove that △ ABC is similar to △ AMP.

(ii) If AC = 10 cm, AP = 12 cm, AM = 7.2 cm and PM = 9.6 cm; find BC and AB.

(i) In △ ABC and △ AMP,

⇒ ∠ABC = ∠AMP (Both equal to 90°)

⇒ ∠BAC = ∠PAM (Common angle)

∴ △ ABC ~ △ AMP (By A.A. axiom)

Hence, proved that △ ABC ~ △ AMP.

(ii) We know that,

Corresponding sides of similar triangles are proportional.

$\therefore \dfrac{AB}{AM} = \dfrac{AC}{AP} \\[1em] \Rightarrow \dfrac{AB}{7.2} = \dfrac{10}{12} \\[1em] \Rightarrow AB = \dfrac{10 \times 7.2}{12} \\[1em] \Rightarrow AB = \dfrac{72}{12} = 6\text{ cm}.$

Also,

$\therefore \dfrac{BC}{PM} = \dfrac{AC}{AP} \\[1em] \Rightarrow \dfrac{BC}{9.6} = \dfrac{10}{12} \\[1em] \Rightarrow BC = \dfrac{10 \times 9.6}{12} \\[1em] \Rightarrow BC = \dfrac{96}{12} = 8\text{ cm}.$

Hence, AB = 6 cm and BC = 8 cm.