Mathematics
For the given frequency distribution, find the:
(a) mean, to the nearest whole number
(b) median
| x | f |
|---|---|
| 10 | 3 |
| 11 | 2 |
| 12 | 2 |
| 13 | 6 |
| 14 | 3 |
| 15 | 5 |
| 16 | 3 |
Measures of Central Tendency
37 Likes
Answer
| x | f | fx |
|---|---|---|
| 10 | 3 | 30 |
| 11 | 2 | 22 |
| 12 | 2 | 24 |
| 13 | 6 | 78 |
| 14 | 3 | 42 |
| 15 | 5 | 75 |
| 16 | 3 | 48 |
| Total | Σf = 24 | Σfx = 319 |
(a) By formula,
Hence, required mean = 13.
(b) Cumulative frequency table :
| x | f | cf |
|---|---|---|
| 10 | 3 | 3 |
| 11 | 2 | 5 (3 + 2) |
| 12 | 2 | 7 (5 + 2) |
| 13 | 6 | 13 (7 + 6) |
| 14 | 3 | 16 (13 + 3) |
| 15 | 5 | 21 (16 + 5) |
| 16 | 3 | 24 (21 + 3) |
Median
Here, total frequency (N) = 24 and .
From the cumulative column,
For 8th to 13th term, the value of x = 13.
Hence, median = 13.
Answered By
8 Likes
Related Questions
Refer to the given bill. A customer paid ₹2,000 (rounded off to the nearest ₹10) to clear the bill.
Note: 5% discount is applicable on an article if 10 or more such articles are purchased.
Article M.P.(₹) Quantity G.S.T A 190 06 12% B 50 12 18% Check whether the total amount paid by the customer is correct or not. Justify your answer with necessary working.
A man bought ₹200 shares of a company at 25% premium. If he received a return of 5% on his investment. Find the :
(a) market value
(b) dividend percent declared
(c) number of shares purchased, if annual dividend is ₹1,000.
Mr. and Mrs. Das were traveling by car from Delhi to Kasauli for a holiday. Distance between Delhi and Kasauli is approximately 350 km (via NH 152D). Due to heavy rain they had to slow down. The average speed of the car was reduced by 20 km/hr and time of the journey increased by 2 hours. Find:
(a) the original speed of the car.
(b) with the reduced speed, the number of hours they took to reach their destination.
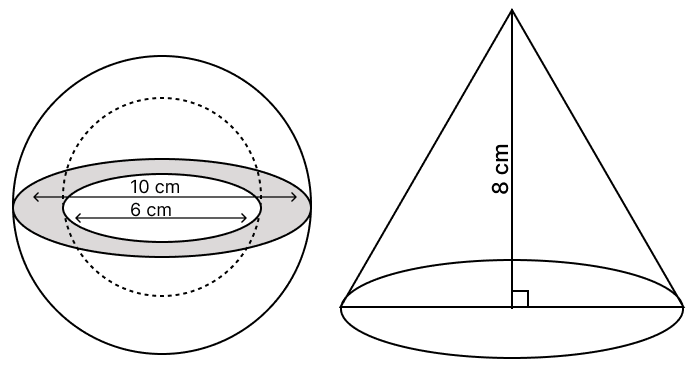
A hollow sphere of external diameter 10 cm and internal diameter 6 cm is melted and made into a solid right circular cone of height 8 cm. Find the radius of the cone so formed.
(Use )