Mathematics
Mr. and Mrs. Das were traveling by car from Delhi to Kasauli for a holiday. Distance between Delhi and Kasauli is approximately 350 km (via NH 152D). Due to heavy rain they had to slow down. The average speed of the car was reduced by 20 km/hr and time of the journey increased by 2 hours. Find:
(a) the original speed of the car.
(b) with the reduced speed, the number of hours they took to reach their destination.
Quadratic Equations
39 Likes
Answer
(a) Let the original speed be x km/hr.
Distance = 350 km
In first case (original speed):
Time hrs
In second case (reduced speed):
Speed = (x - 20) km/hr
Time hrs
According to the question,
Time taken to reach destination increases by 2 hours in the second case.
Since speed cannot be negative, x = 70 km/hr.
Hence, original speed of the car = 70 km/hr.
(b) Reduced Speed = x - 20 = 70 - 20 = 50 km/hr.
Time taken with reduced speed = 7 hours.
Hence, with reduced speed the time taken to reach destination = 7 hours.
Answered By
15 Likes
Related Questions
A man bought ₹200 shares of a company at 25% premium. If he received a return of 5% on his investment. Find the :
(a) market value
(b) dividend percent declared
(c) number of shares purchased, if annual dividend is ₹1,000.
For the given frequency distribution, find the:
(a) mean, to the nearest whole number
(b) median
x f 10 3 11 2 12 2 13 6 14 3 15 5 16 3 A hollow sphere of external diameter 10 cm and internal diameter 6 cm is melted and made into a solid right circular cone of height 8 cm. Find the radius of the cone so formed.
(Use )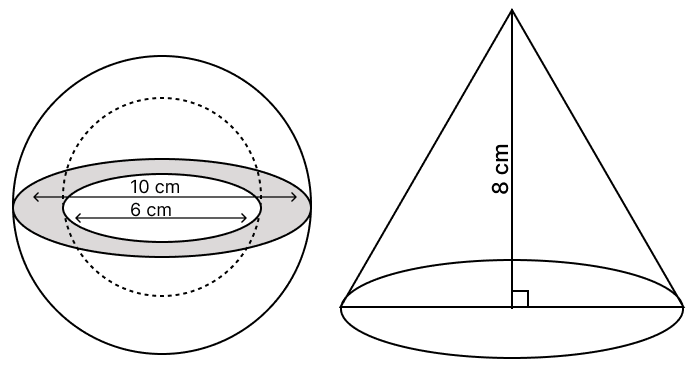
Ms. Sushmita went to a fair and participated in a game. The game consisted of a box having number cards with numbers from 01 to 30. The three prizes were as per the given table:
Prize Number on the card drawn at random is a Wall clock perfect square Water bottle even number which is also a multiple of 3 Purse prime number Find the probability of winning a:
(a) Wall Clock
(b) Water Bottle
(c) Purse