Mathematics
Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is the mid-point of LN.
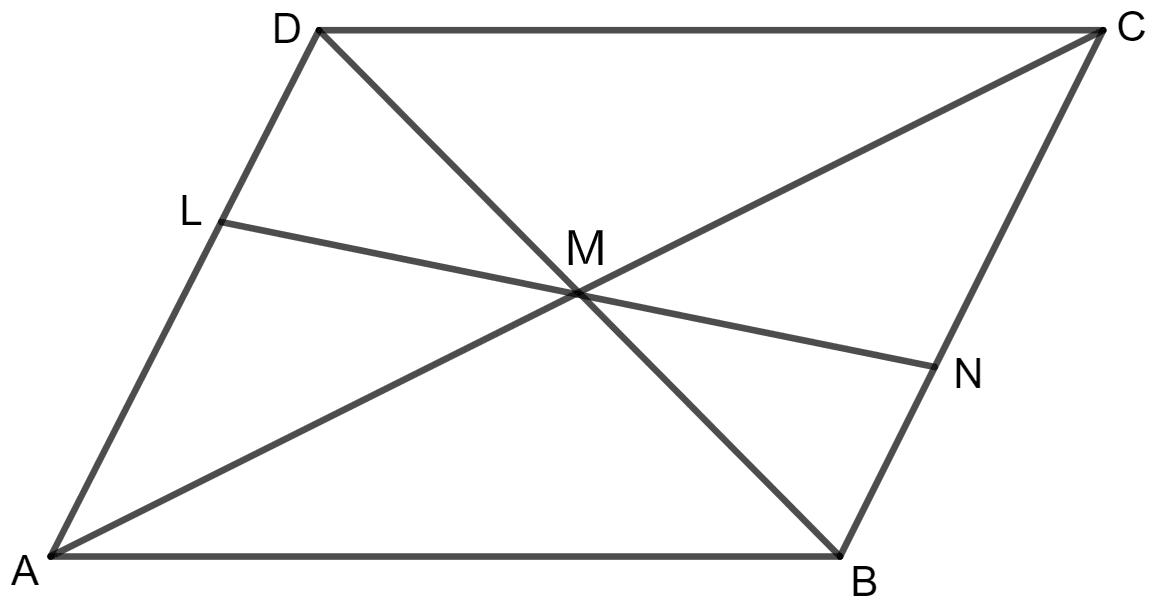
Answer
According to the properties of a parallelogram, the diagonals of a parallelogram bisect each other.
⇒ MD = MB
Also, ∠ADB = ∠DBN (∵ alternate angles)
And, ∠DML = ∠BMN (∵ vertically opposite angles)
Hence, by Angle Side Angle congruency,
Δ DML ≅ Δ BMN
By using Corresponding Parts of Congruent Triangles,
LM = MN
∵ M is mid - point of LN.
Hence, M is the mid-point of LN
Related Questions
ABCD is a rhombus. If ∠BCA = 35°, find ∠ADC.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°, find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
In an isosceles-trapezium, show that the opposite angles are supplementary.
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD ?
(ii) AC is perpendicular to BD but is not equal to it ?
(iii) AC = BD but AC is not perpendicular to BD?