Mathematics
ABCD is a rhombus. If ∠BCA = 35°, find ∠ADC.
Quadrilaterals
13 Likes
Answer
In rhombus ABCD, all sides are equal:
AB = BC = CD = DA
Thus, alternate angles are equal:

∠DAC = ∠BCA
It is given that ∠BCA = 35°.
⇒ ∠DAC = ∠BCA = 35°
And, ∠DAC = ∠ACD [as AD = CD]
⇒ 35° = ∠ACD
In triangle ADC, sum of all the angles of triangles is 180°
⇒ ∠DAC + ∠ACD + ∠ADC = 180°
⇒ 35° + 35° + ∠ADC = 180°
⇒ 70° + ∠ADC = 180°
⇒ ∠ADC = 180° - 70°
⇒ ∠ADC = 110°
Hence, the value of ∠ADC is 110°.
Answered By
11 Likes
Related Questions
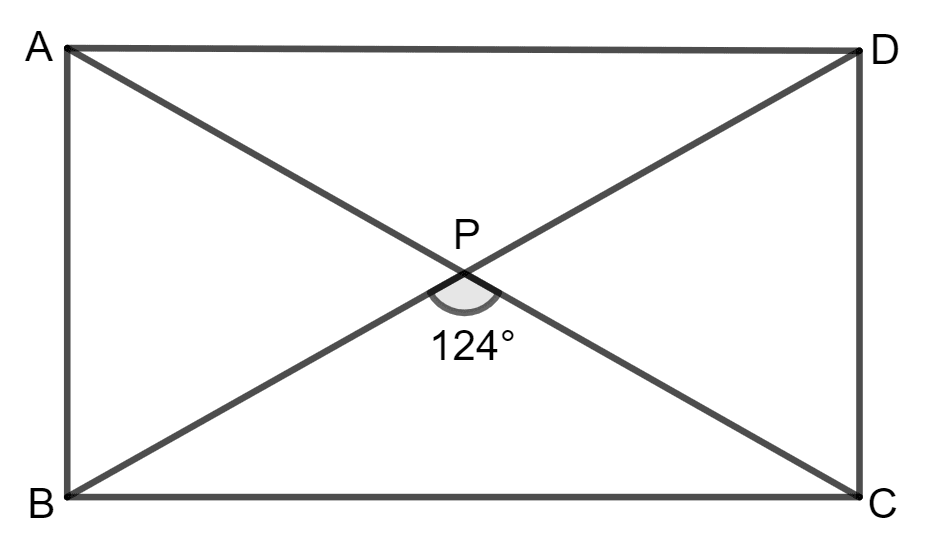
ABCD is a rectangle. If ∠BPC = 124°, calculate :
(i) ∠BAP
(ii) ∠ADP.
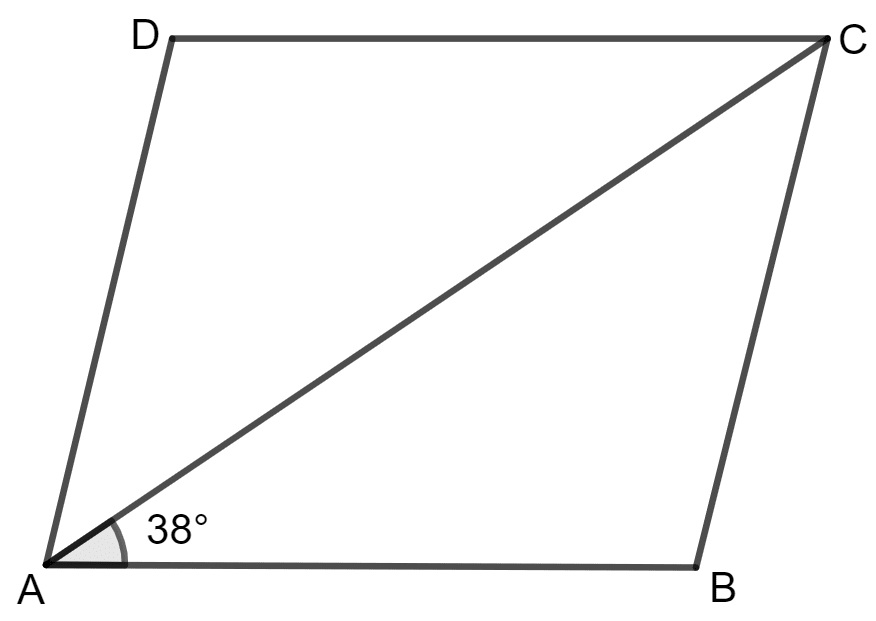
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°, find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is the mid-point of LN.