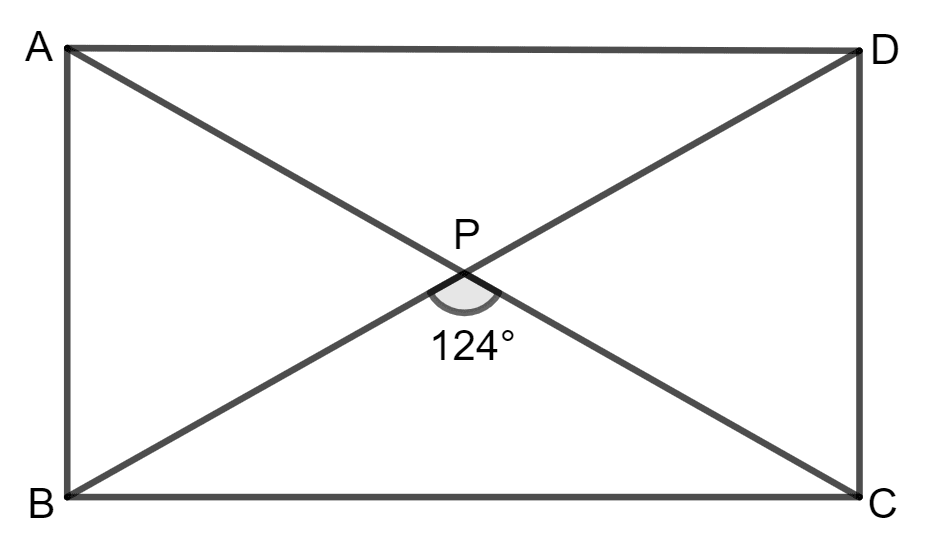
ABCD is a rectangle. If ∠BPC = 124°, calculate :

(i) ∠BAP

(ii) ∠ADP.

Since ABCD is a rectangle, the diagonals bisect each other, and ∠BPC forms two angles at point P.

According to the properties of a rectangle, the diagonals are equal and intersect at the midpoint.

(i) ∠BAP = $\dfrac{1}{2}$ of ∠BPC (since diagonals bisect each other).

So, ∠BAP = $\dfrac{1}{2}$ × 124° = 62°.

Hence, the value of ∠BAP is 62°.

(ii) Diagonals of rectangle are equal and bisect each other.

⇒ ∠PBC = ∠PCB = x (say)

But, in triangle BPC, sum of all the angles are 180°.

⇒ ∠BPC + ∠PBC + ∠PCB = 180°

⇒ 124° + x + x = 180°

⇒ 2x = 180° − 124°

⇒ 2x = 56°

⇒ x = 28°

⇒ ∠PBC = 28°

But ∠PBC = ∠ADP [alternate angles]

∠ADP = 28°

Hence, the value of ∠ADP is 28°.