Mathematics
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate (i) the x-axis (ii) the y-axis and (iii) the origin.
Answer
Given, Q is the image of P on reflection in y-axis and midpoint of PQ is invariant on reflection in x-axis.
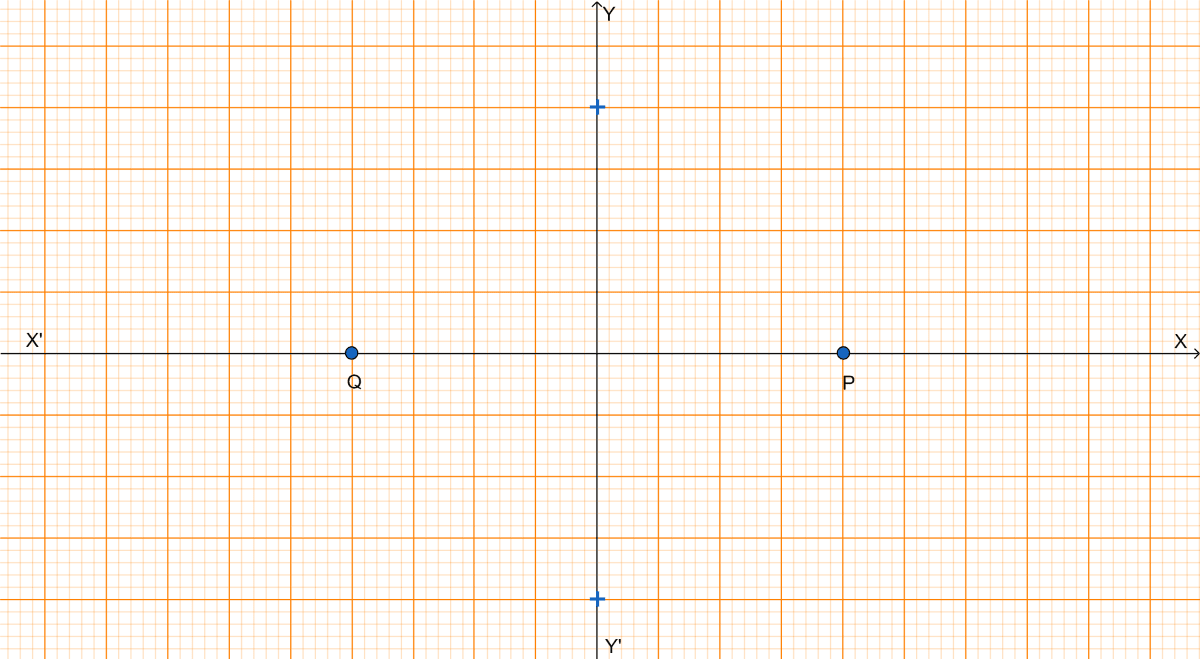
From graph we get,
(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of the line segment PQ is the y-axis.
(iii) The origin will be the mid point of the line segment PQ.
Related Questions
The triangle ABC where A(1, 2), B(4, 8), C(6, 8) is reflected in the x-axis to triangle A'B'C'. The triangle A'B'C' is then reflected in the origin to the triangle A''B''C''. Write down the coordinates of A'', B'', C''. Write down a single transformation that maps ABC onto A''B''C''.
The image of a point P on reflection in a line l is a point P'. Describe the location of the line l.
The point (-3, 0) on reflection in a line is mapped as (3, 0) and the point (2, -3) on reflection in the same line is mapped as (-2, -3).
(i) Name the mirror line.
(ii) Write the coordinates of the image of (-3, -4) in the mirror line.
Use graph paper for this question.
Take 2 cm = 1 unit on both the axes.
(i) Plot the points A(0, 4), B(2, 2), C(5, 2) and D(4, 0), E(0, 0) is the origin.
(ii) Reflect B, C, D on the y-axis and name them as B', C' and D' respectively.
(iii) Join the points ABCDD'B'C' and A in order and give a geometrical name to the closed figure.