Mathematics
If a polynomial x3 + 2x2 – ax + b leaves a remainder -6 when divided by x + 1 and the same polynomial has x - 2 as a factor, then find the values of a and b.
Factorisation
21 Likes
Answer
Given,
x3 + 2x2 – ax + b leaves a remainder -6 when divided by x + 1.
⇒ x + 1 = 0
⇒ x = -1.
Let f(x) = x3 + 2x2 – ax + b, then f(-1) = -6.
⇒ f(-1) = -6
⇒ (-1)3 + 2(-1)2 - a(-1) + b = -6
⇒ -1 + 2(1) + a + b = -6
⇒ -1 + 2 + a + b = -6
⇒ a + b + 1 = -6
⇒ a + b = -6 - 1
⇒ a + b = -7 ……..(1)
Given ,
x - 2 is a factor of f(x).
⇒ x - 2 = 0
⇒ x = 2.
f(2) = 0
⇒ 23 + 2(2)2 – 2a + b = 0
⇒ 8 + 2(4) - 2a + b = 0
⇒ 8 + 8 - 2a + b = 0
⇒ 16 - 2a + b = 0
⇒ 2a - b = 16 ……(2)
Adding equation (1) and (2), we get :
⇒ a + b + 2a - b = -7 + 16
⇒ 3a = 9
⇒ a = = 3.
Substituting value of a = 3 in equation (1), we get :
⇒ 3 + b = -7
⇒ b = -7 - 3 = -10.
Hence, a = 3 and b = -10.
Answered By
10 Likes
Related Questions
The data given below shows the marks of 12 students in a test, arranged in ascending order :
2, 3, 3, 3, 4, x, x + 2, 8, p, q, 8, 9.
If the given value of the median and mode is 6 and 8 respectively, then find the values of x, p, q.
Solve the linear inequation, write down the solution set and represent it on the real number line :
5(2 - 4x) > 18 - 16x > 22 - 20x, x ∈ R
If A =
(a) Is the product AC possible? Justify your answer.
(b) Find the matrix X, such that X = AB + B2 − DC
In the given figure (not drawn to scale), BC is parallel to EF, CD is parallel to FG, AE : EB = 2 : 3, ∠BAD = 70°, ∠ACB = 105°, ∠ADC = 40° and AC is bisector of ∠BAD.
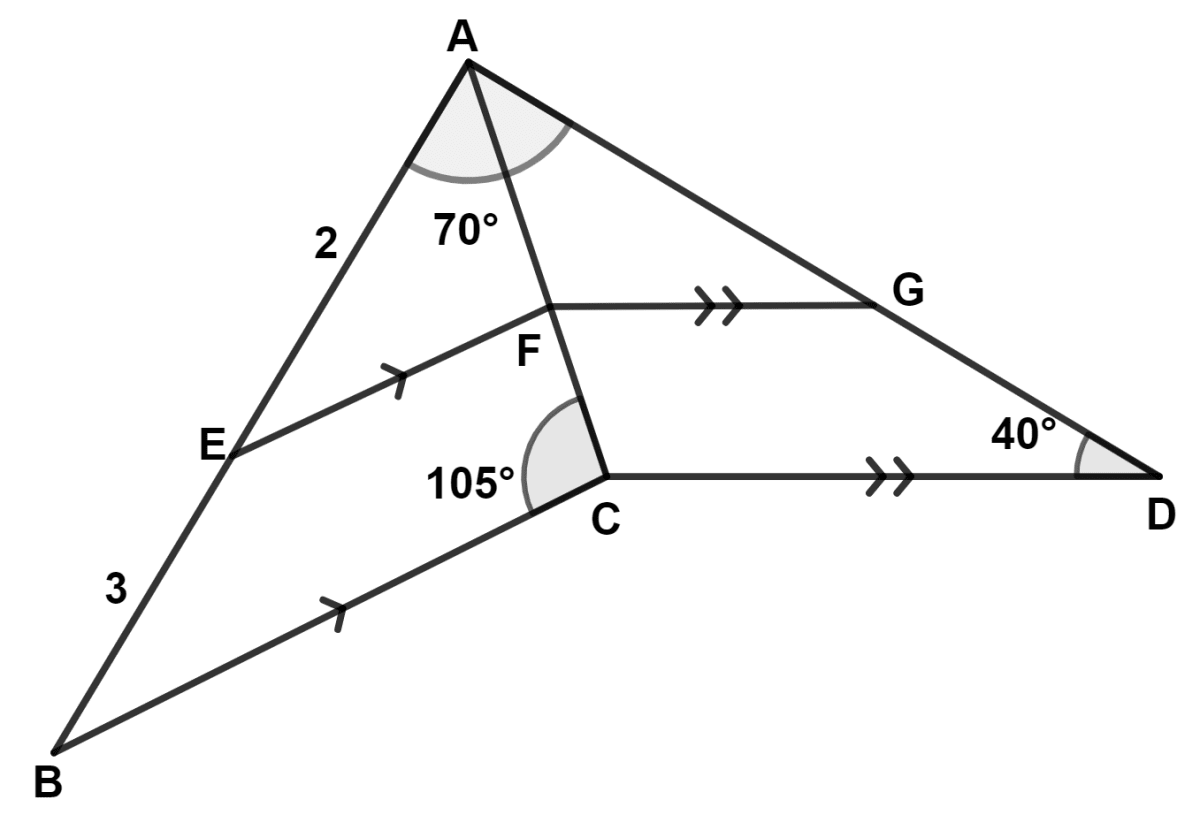
(a) Prove Δ AEF ~ Δ AGF
(b) Find :
(i) AG : AD
(ii) area of Δ ACB: area Δ ACD
(iii) area of quadrilateral ABCD: area of Δ ACB.