Mathematics
The data given below shows the marks of 12 students in a test, arranged in ascending order :
2, 3, 3, 3, 4, x, x + 2, 8, p, q, 8, 9.
If the given value of the median and mode is 6 and 8 respectively, then find the values of x, p, q.
Statistics
43 Likes
Answer
By formula,
Median =
Substituting values we get :
Numbers :
2, 3, 3, 3, 4, 5, 7, 8, p, q, 8, 9.
Since, mode = 8, it means 8 occurs for the most times in the series.
Since, 3 occurs 3 times in the series,
∴ 8 must occur for atleast 4 times in order to be the mode.
∴ p = q = 8.
Hence, x = 5, p = 8 and q = 8.
Answered By
23 Likes
Related Questions
The curved surface area of a right circular cone is half of another right circular cone. If the ratio of their slant heights is 2 : 1 and that of their volumes is 3 : 1, find ratio of their:
(a) radii
(b) heights
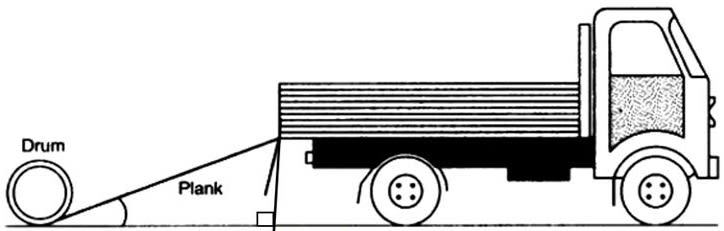
A cylindrical drum is unloaded from a truck by rolling it down along a wooden plank. The length of the plank is 10 m and it is making an angle of 10° with the horizontal ground. Find the height from which the cylindrical drum was rolled down. Give your answer correct to 3 significant figures.
Solve the linear inequation, write down the solution set and represent it on the real number line :
5(2 - 4x) > 18 - 16x > 22 - 20x, x ∈ R
If a polynomial x3 + 2x2 – ax + b leaves a remainder -6 when divided by x + 1 and the same polynomial has x - 2 as a factor, then find the values of a and b.