Mathematics
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle, show that the diagonals AC and BD intersect at right angle.
Mid-point Theorem
27 Likes
Answer
Let ABCD be a quadrilateral and P, Q, R and S are the mid-point of AB, BC, CD and DA.
Diagonal AC and BD intersect at point O.
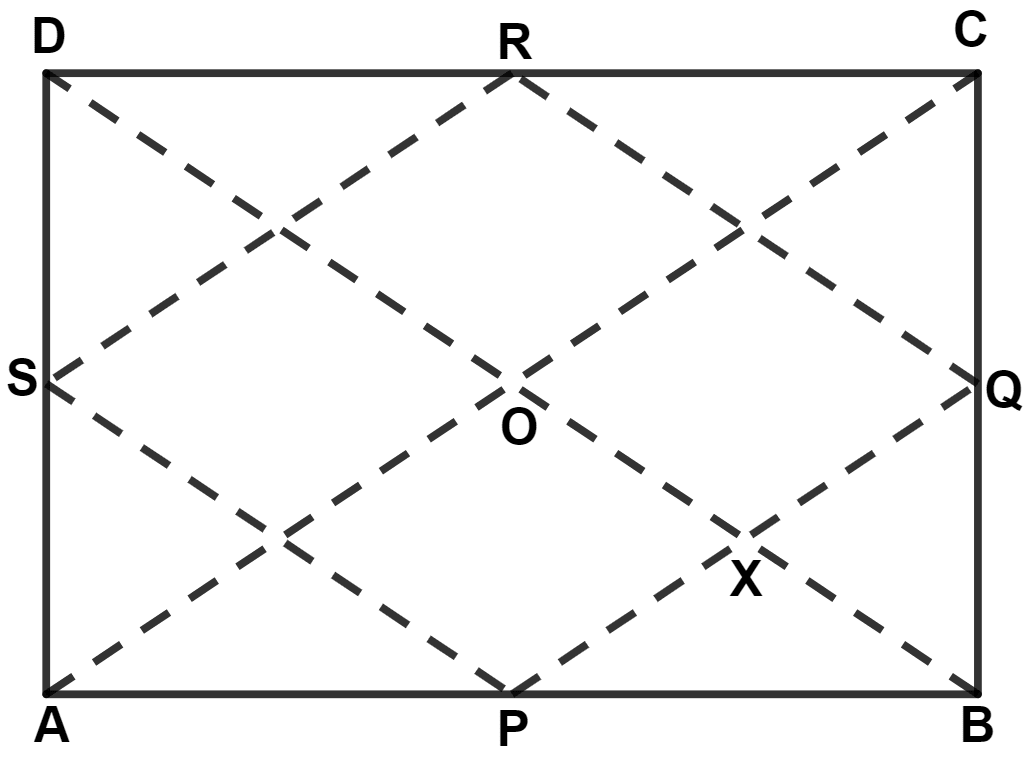
By mid-point theorem,
The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.
In △ ABC,
P and Q are mid-points of AB and BC.
∴ PQ || AC (By mid-point theorem)
From figure,
⇒ ∠AOD = ∠PXO (Corresponding angles are equal) …………(1)
In △ BCD,
R and Q are mid-points of CD and BC.
∴ QR || BD (By mid-point theorem)
Interior angles of a rectangle equals to 90°.
⇒ ∠RQX = ∠Q = 90°.
From figure,
⇒ ∠PXO = ∠RQX = 90° (Corresponding angles are equal) …………(2)
From (1) and (2), we get :
⇒ ∠AOD = ∠PXO = 90°.
Hence, AC and BD intersect at right angles.
Answered By
15 Likes
Related Questions
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet side BC at points M and N respectively. Prove that :
BM = MN = NC.
In triangle ABC; M is the mid-point of AB, N is mid-point of AC and D is any point in base BC. Use intercept theorem to show that MN bisects AD.
The midpoint of the side of a triangle are joined together to get four triangles. These four triangles are:
not equal to each other
congruent to each other
not congruent to each other
none of these
In the given figure, AB || CD || EF. If AC = 7 cm, AE = 14 cm and BF = 20 cm, then DF is equal to:
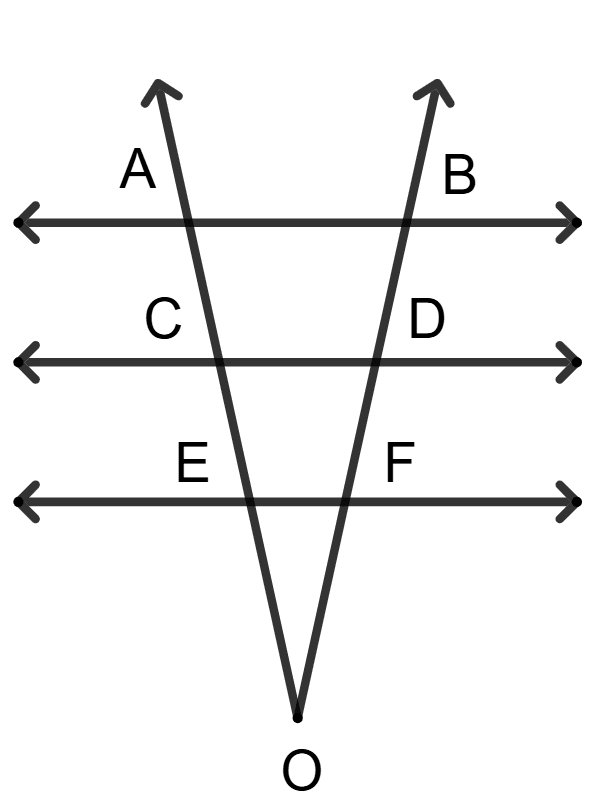
7 cm
14 cm
10 cm
16 cm