Mathematics
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Related Questions
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
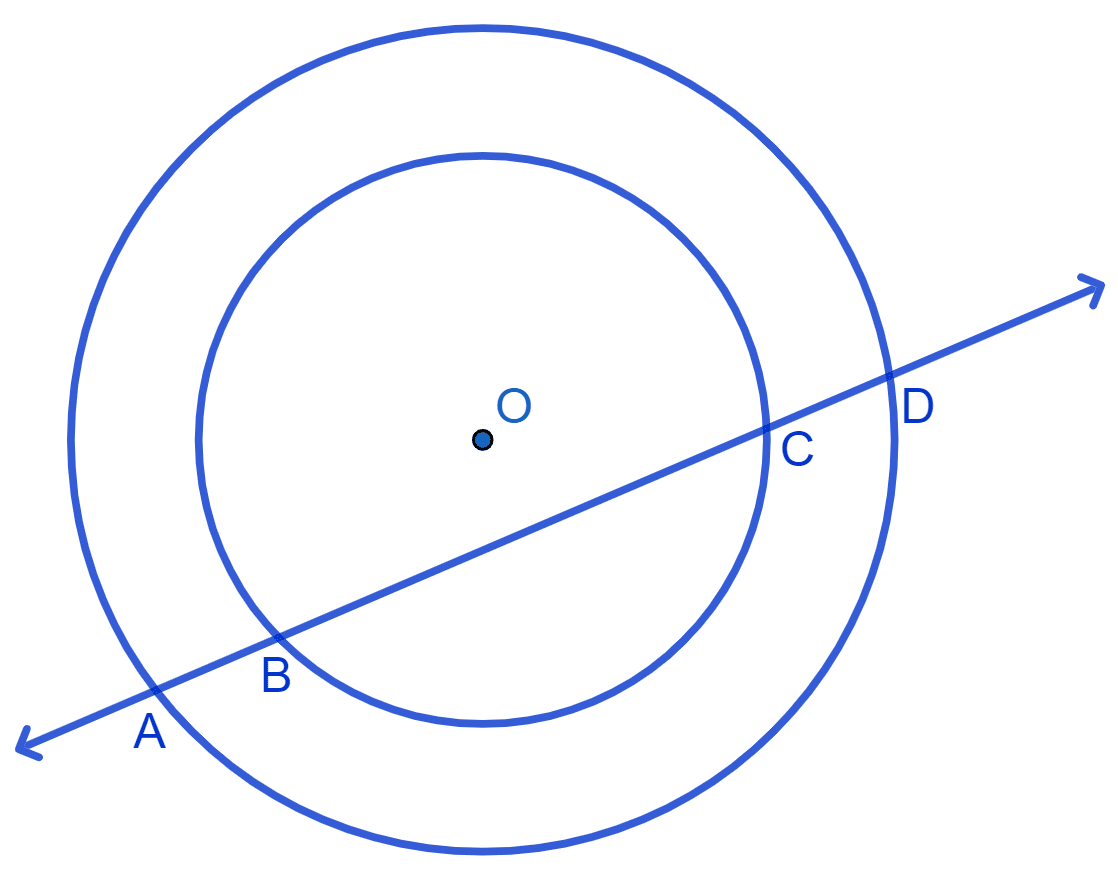
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD.