Mathematics
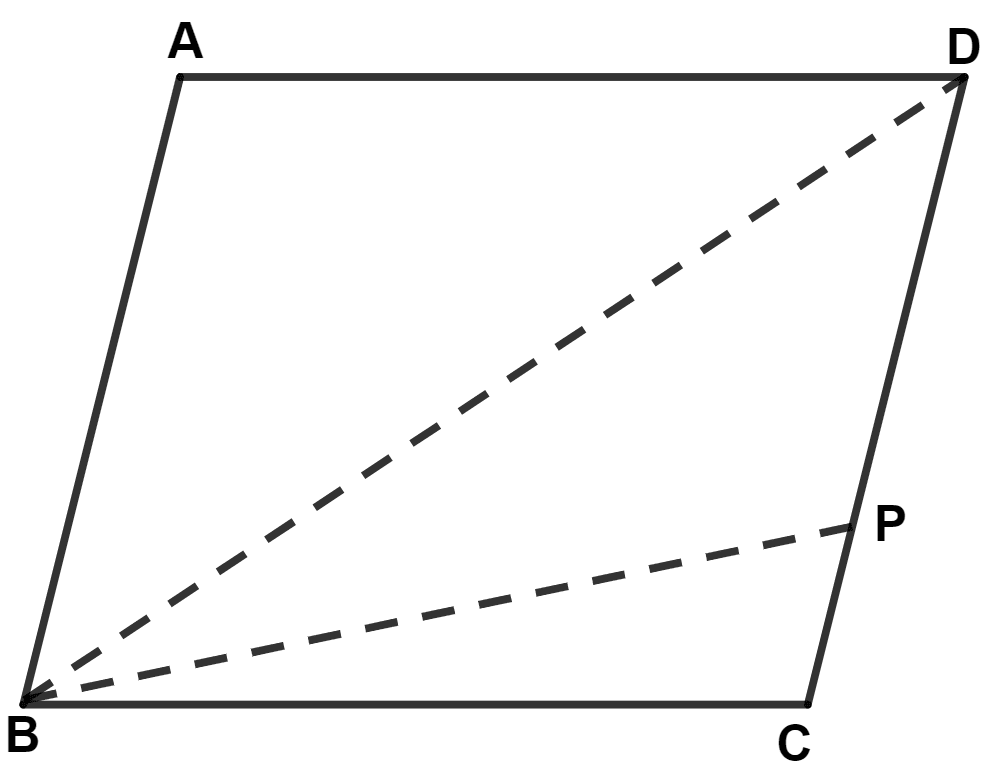
In a parallelogram ABCD, point P lies in DC such that DP : PC = 3 : 2. If area of Δ DPB = 30 sq.cm, find the area of the parallelogram ABCD.
Theorems on Area
10 Likes
Answer
Given,
DP : PC = 3 : 2
We know that,
Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.
From figure,
Area of Δ CDB = Area of Δ PCB + Area of Δ DPB = 20 + 30 = 50 cm2.
Since, diagonal divides a || gm into two triangles of equal area.
∴ Area of || gm ABCD = 2 Area of Δ CDB = 2 × 50 = 100 cm2.
Hence, area of \\ gm ABCD = 100 cm2.
Answered By
7 Likes
Related Questions
ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD respectively. Prove that area of triangle APQ = of the area of parallelogram ABCD.
The base BC of triangle ABC is divided at D so that BD = DC.
Prove that the area of Δ ABD = of the area of Δ ABC.
The median of a triangle divides it into two:
triangles of equal area
congruent triangles
right triangles
isosceles triangles
The area of given parallelogram is:
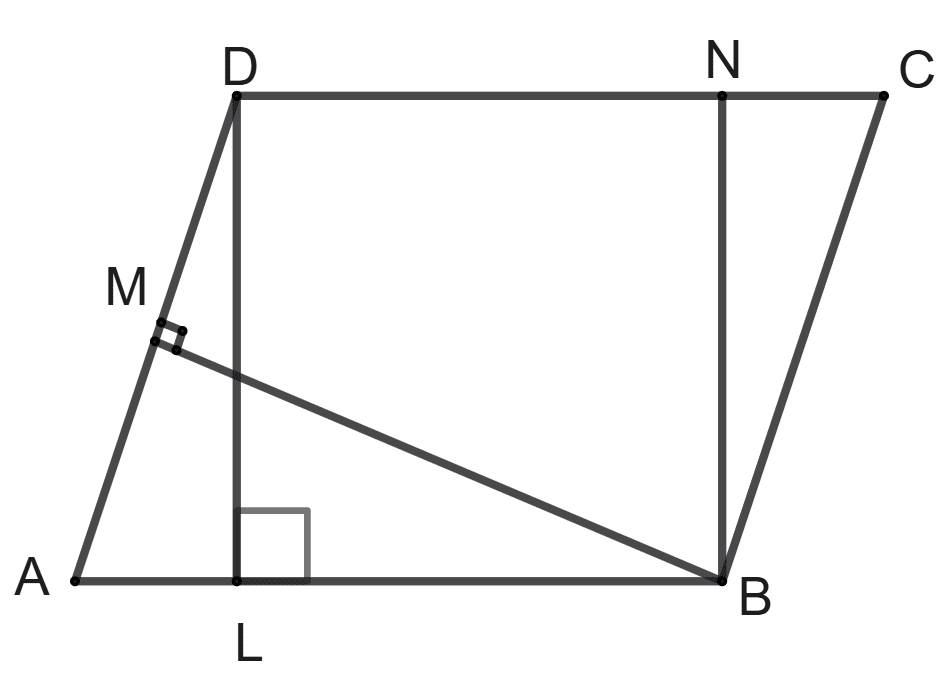
AB x BM
BC x BN
DC x DL
AD x DL