Mathematics
In a triangle ABC, AB = AC and ∠A = 36°. If the internal bisector of ∠C meets AB at point D, prove that AD = BC.
Triangles
15 Likes
Answer
In △ ABC,
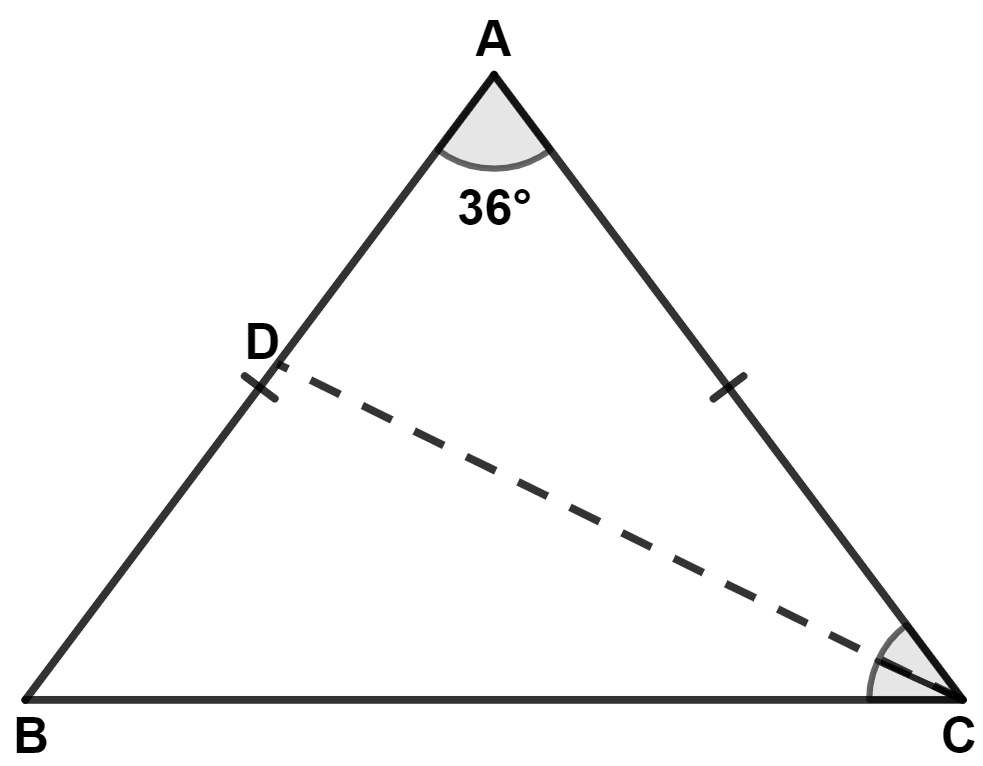
⇒ AB = AC (Given)
∴ ∠B = ∠C = x (let) [Angles opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠A + ∠B + ∠C = 180°
⇒ 36° + x + x = 180°
⇒ 36° + 2x = 180°
⇒ 2x = 180° - 36°
⇒ 2x = 144°
⇒ x = = 72°.
Since, CD is bisector of angle C,
∴ ∠ACD = ∠BCD = = 36°.
In △ ACD,
⇒ ∠ACD = ∠DAC (Both equal to 36°)
∴ AD = DC [Sides opposite to equal angles are equal] ……..(1)
In △ DCB,
By angle sum property of triangle,
⇒ ∠CDB + ∠DCB + ∠DBC = 180°
⇒ ∠CDB + 36° + 72° = 180°
⇒ ∠CDB + 108° = 180°
⇒ ∠CDB = 180° - 108° = 72°.
∴ ∠CDB = ∠DBC (Both equal to 72°)
∴ BC = CD (Sides opposite to equal angles are equal) ………..(2)
From equation (1) and (2), we get :
⇒ AD = BC.
Hence, proved that AD = BC.
Answered By
11 Likes
Related Questions
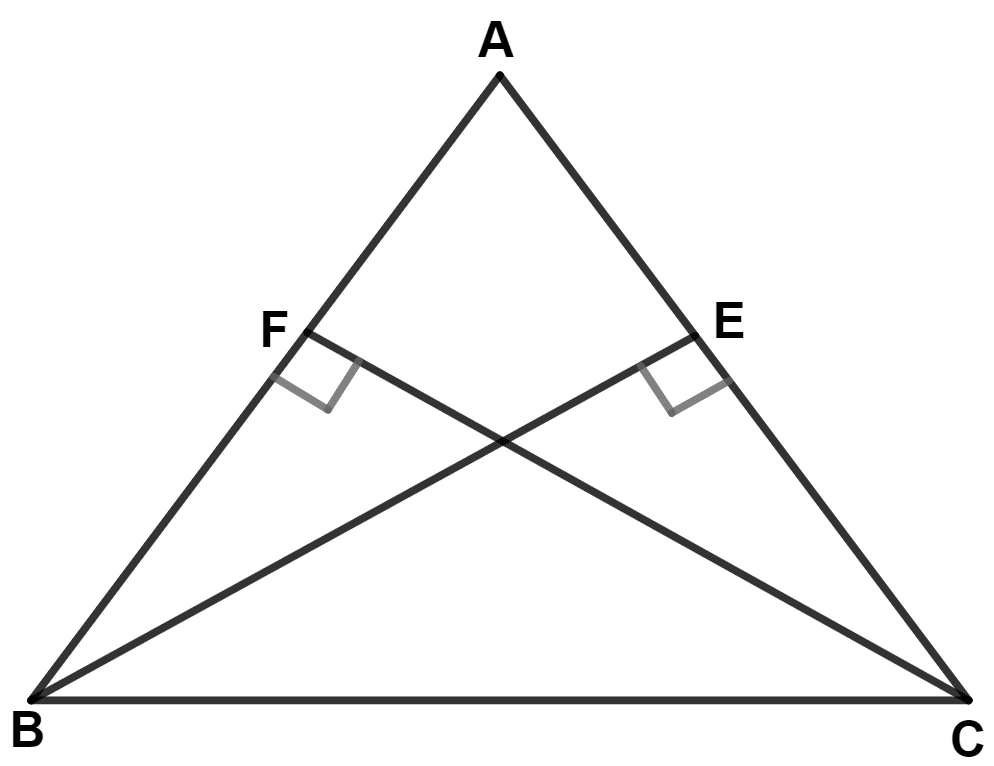
In triangle ABC, AB = AC; BE ⊥ AC and CF ⊥ AB. Prove that :
(i) BE = CF
(ii) AF = AE
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD. Prove that : ∠BCD = 90°.
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
Prove that the bisectors of the base angles of an isosceles triangle are equal.