Mathematics
In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.
Triangles
33 Likes
Answer
△ ABC is shown below:
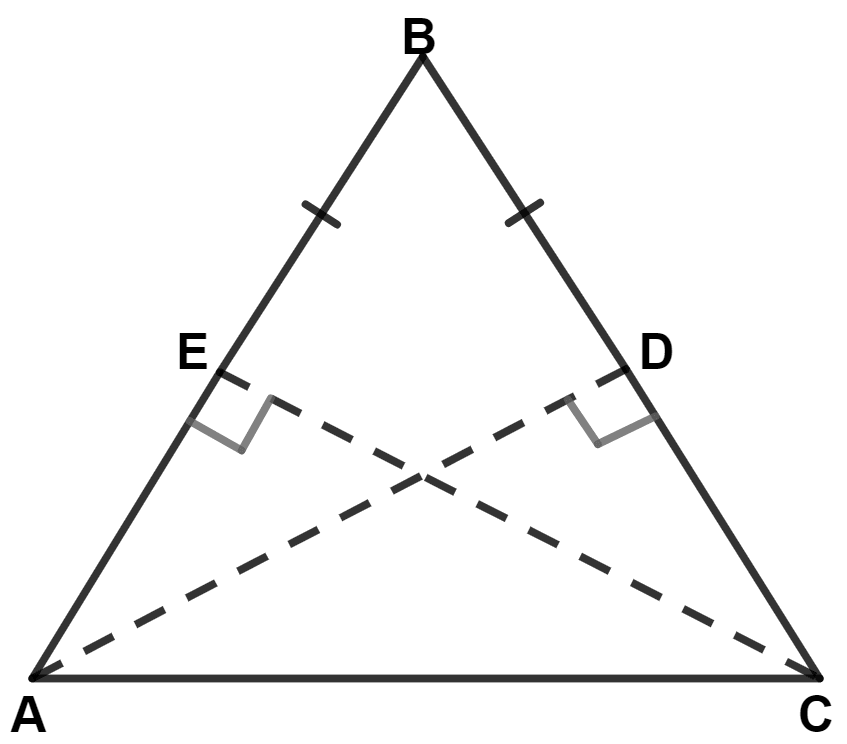
In △ ABD and △ CBE,
⇒ ∠B = ∠B (Common angle)
⇒ ∠ADB = ∠CEB (Both equal to 90°)
⇒ AB = BC (Given)
∴ △ ABD ≅ △ CBE (By A.A.S. axiom).
We know that,
Corresponding parts of congruent triangles are equal.
∴ AD = CE
Hence, proved that AD = CE.
Answered By
22 Likes
Related Questions
In the following figure, OA = OC and AB = BC. Prove that :
(i) ∠AOB = 90°
(ii) △ AOD ≅ △ COD
(iii) AD = CD

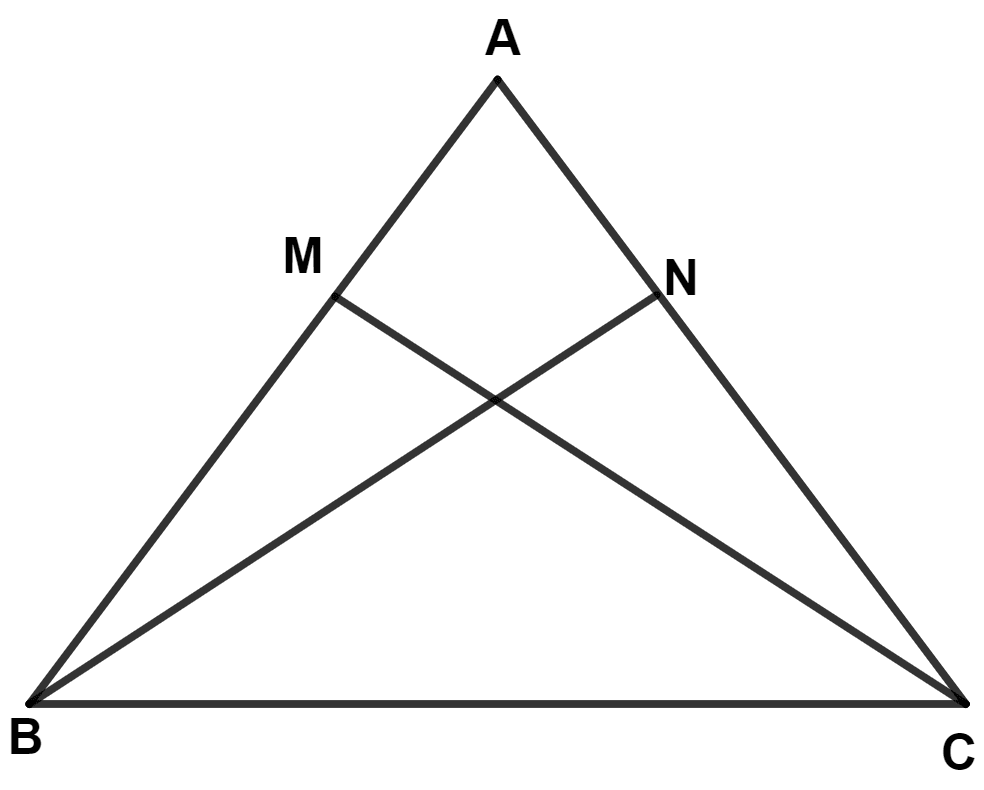
The following figure shows a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that :
(i) AM = AN
(ii) △ AMC ≅ △ ANB
(iii) BN = CM
(iv) △ BMC ≅ △ CNB
In triangles ABC and PQR, ∠A = ∠Q and ∠B = ∠R. In order to make these triangles congruent, we must have AB equal to:
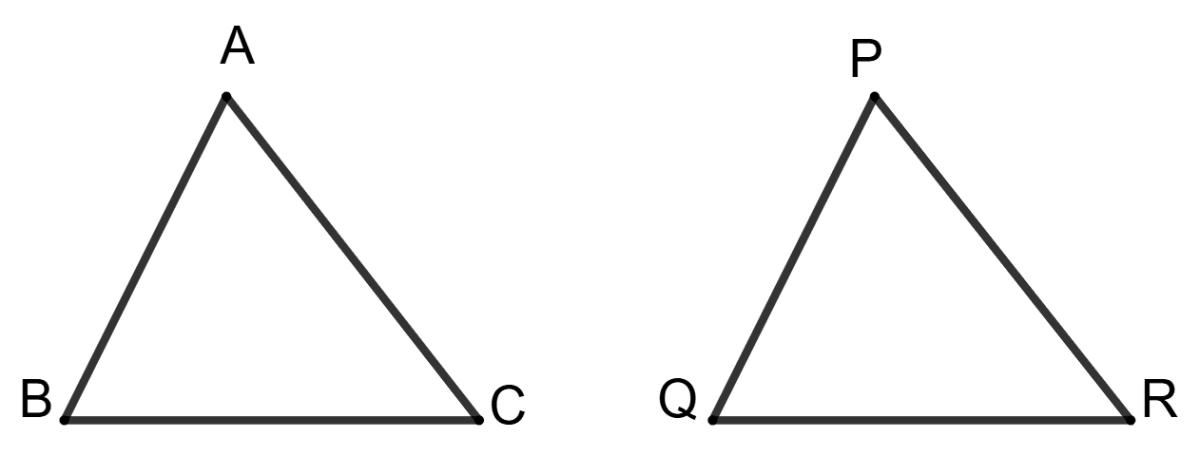
PQ
PR
QR
none of these
If two sides and an angle of one triangle are equal to two sides and an angle of the other triangle, then the triangle must be congruent
no
yes
can't say