Mathematics
In the following figure, OA = OC and AB = BC. Prove that :
(i) ∠AOB = 90°
(ii) △ AOD ≅ △ COD
(iii) AD = CD

Triangles
30 Likes
Answer
(i) In △ AOB and △ COB,
⇒ OA = OC (Given)
⇒ AB = BC (Given)
⇒ OB = OB (Common side)
∴ △ AOB ≅ △ COB (By S.S.S. axiom).
We know that,
Corresponding parts of congruent triangles are equal.
∴ ∠AOB = ∠COB = x (let)
From figure,
AC is a straight line.
∴ ∠AOB + ∠COB = 180°
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = = 90°.
∴ ∠AOB = 90°.
Hence, proved that ∠AOB = 90°.
(ii) We know that,
Vertically opposite angles are equal.
∴ ∠AOD = ∠COB = 90° and ∠COD = ∠AOB = 90°.
In △ AOD and △ COD,
⇒ OA = OC (Given)
⇒ ∠AOD = ∠COD (Both equal to 90°)
⇒ OD = OD (Common side)
∴ △ AOD ≅ △ COD (By S.A.S. axiom).
Hence, proved that △ AOD ≅ △ COD.
(iii) Since, △ AOD ≅ △ COD.
We know that,
Corresponding parts of congruent triangles are equal.
∴ AD = CD
Hence, proved that AD = CD.
Answered By
17 Likes
Related Questions
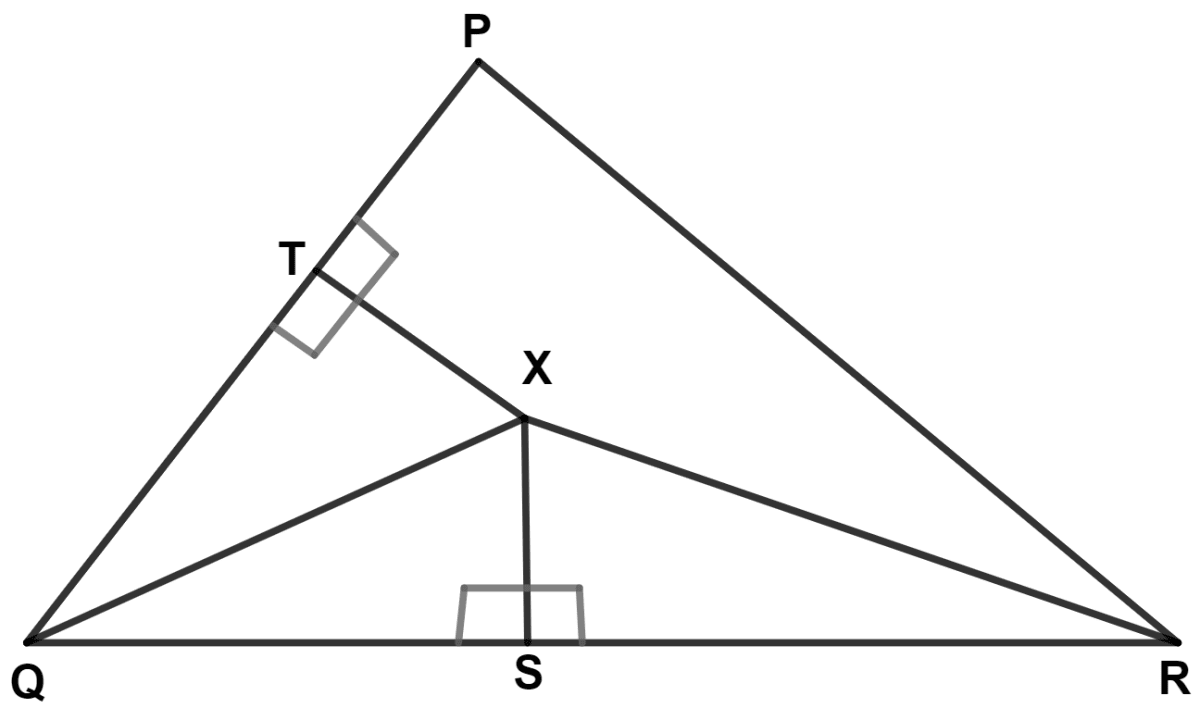
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR. If XS ⊥ QR and XT ⊥ PQ; prove that :
(i) △ XTQ ≅ △ XSQ
(ii) PX bisects angle P.
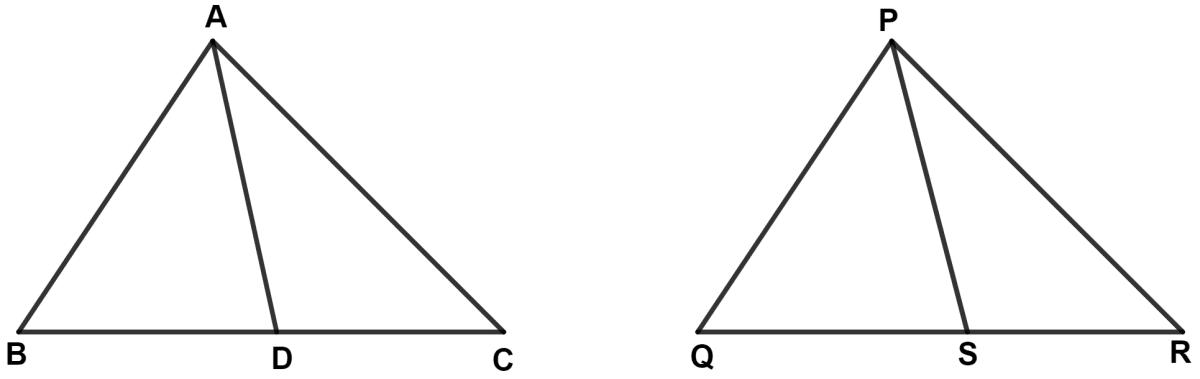
In the following figures, the sides AB and BC and the median AD of the triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that △ ABC and △ PQR are congruent.
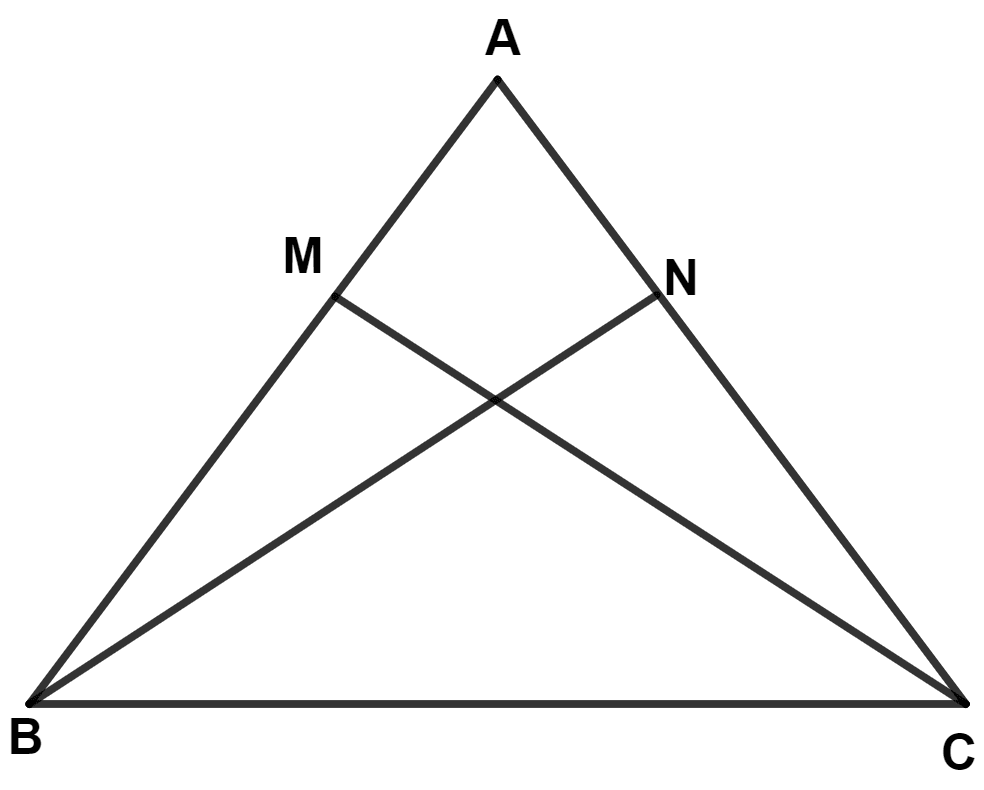
The following figure shows a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that :
(i) AM = AN
(ii) △ AMC ≅ △ ANB
(iii) BN = CM
(iv) △ BMC ≅ △ CNB
In a triangle ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB. Prove that : AD = CE.