Mathematics
In Δ ABC, D is a point on BC such that AB = AD = BD = DC. Show that :
∠ADC : ∠C = 4 : 1.
Triangles
10 Likes
Answer
Given,
AB = AD = BD
∴ Δ ABD is an equilateral triangle.
∴ ∠ABD = ∠ADB = ∠BAD = 60°.
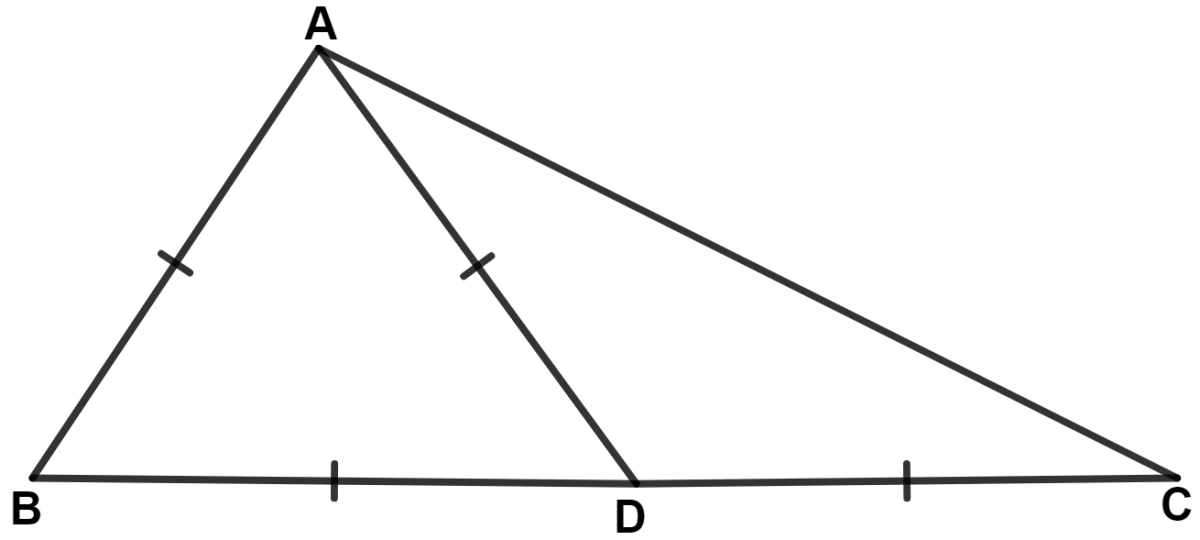
Since, BDC is a straight line.
∴ ∠ADB + ∠ADC = 180°
⇒ 60° + ∠ADC = 180°
⇒ ∠ADC = 180° - 60° = 120°.
In Δ ADC,
⇒ AD = DC (Given)
∴ ∠DAC = ∠DCA = x (let) [Angles opposite to equal sides are equal]
By angle sum property of triangle,
⇒ ∠DAC + ∠DCA + ∠ADC = 180°
⇒ x + x + 120° = 180°
⇒ 2x = 180° - 120°
⇒ 2x = 60°
⇒ x = = 30°
⇒ ∠DCA = ∠C = 30°.
⇒ ∠ADC : ∠C = 120° : 30° = 4 : 1.
Hence, proved that ∠ADC : ∠C = 4 : 1.
Answered By
5 Likes
Related Questions
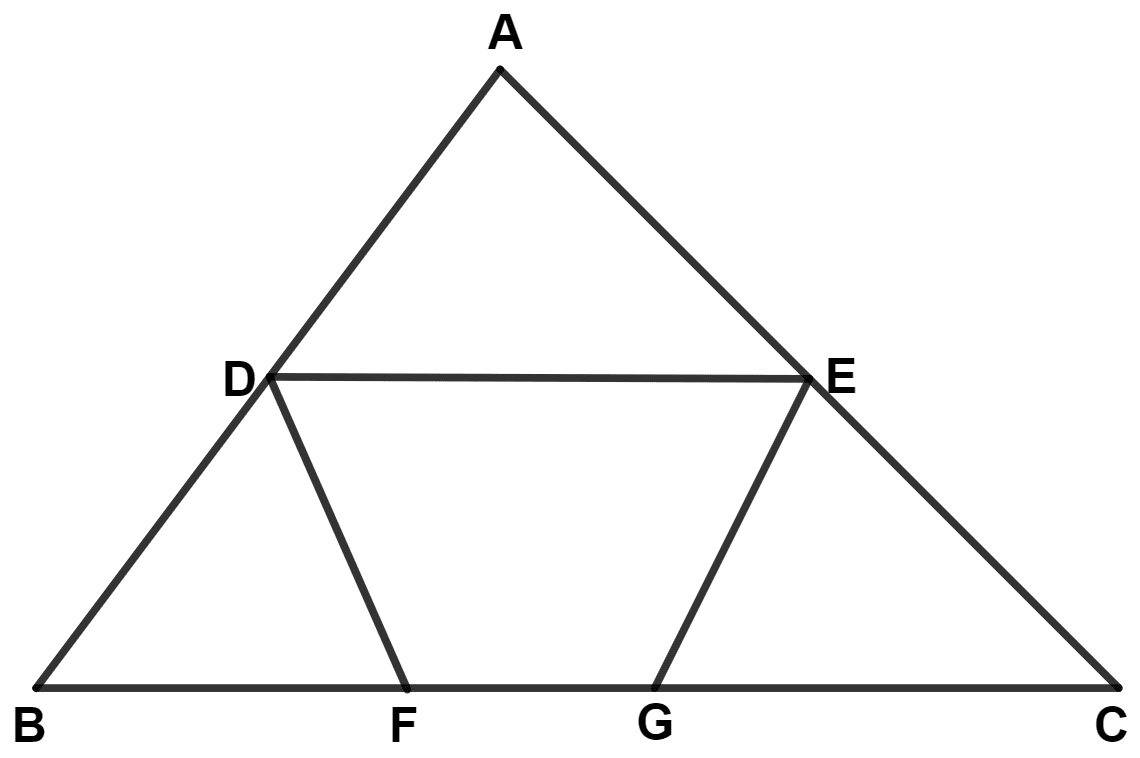
The given figure shows an equilateral triangle ABC with each side 15 cm. Also DE // BC, DF // AC and EG //AB. If DE + DF + EG = 20 cm, find FG.
In triangle ABC, bisector of angle BAC meets opposite side BC at point D. If BD = CD, prove that △ ABC is isosceles.
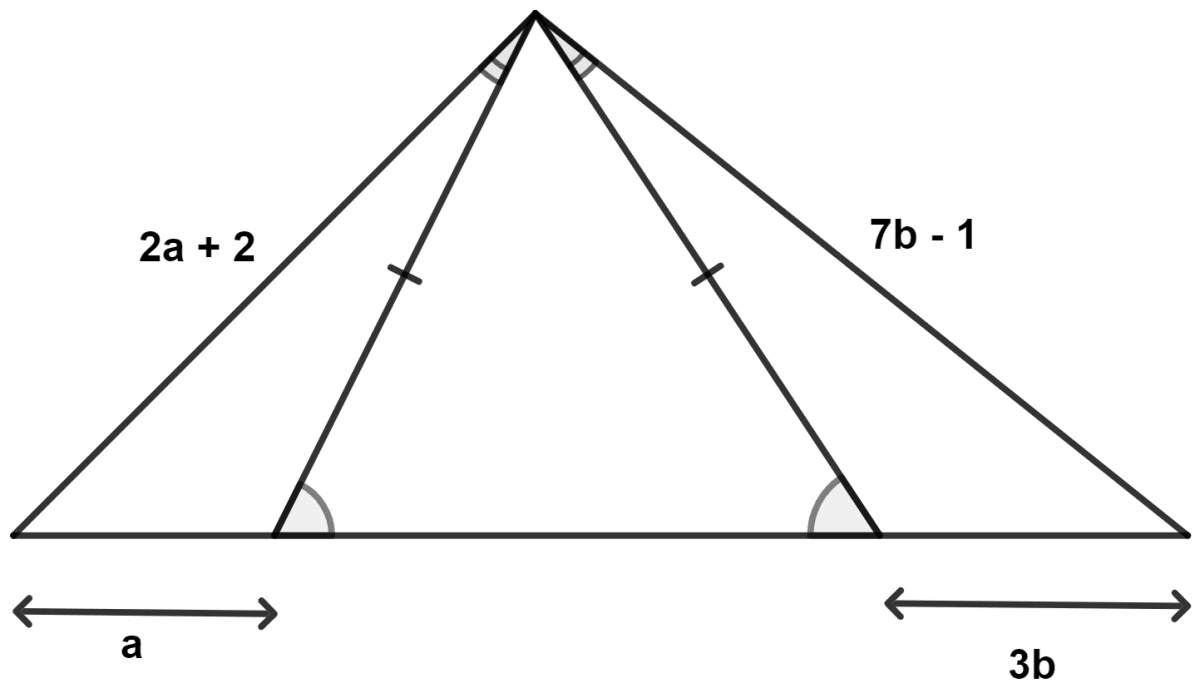
Using the information, given in each of the following figures, find the values of a and b.
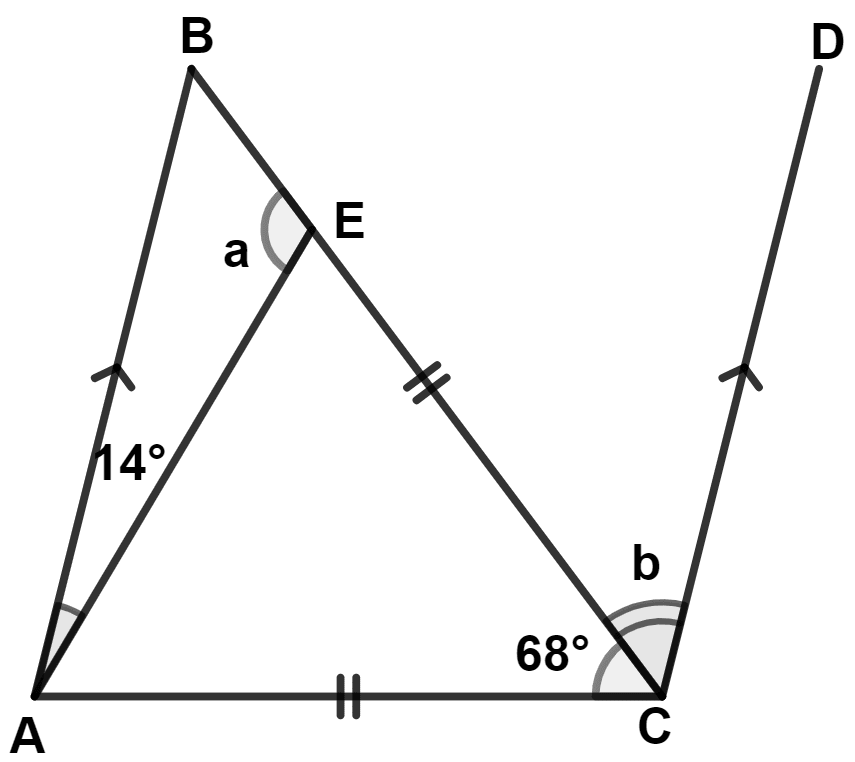
Using the information, given in each of the following figures, find the values of a and b.