Mathematics
In △ ABC, E and F are mid-points of sides AB and AC respectively. If BF and CE intersect each other at point O, prove that the △ OBC and quadrilateral AEOF are equal in area.
Answer
By mid-point theorem,
The line segment in a triangle joining the midpoint of any two sides of the triangle is said to be parallel to its third side and is also half of the length of the third side.
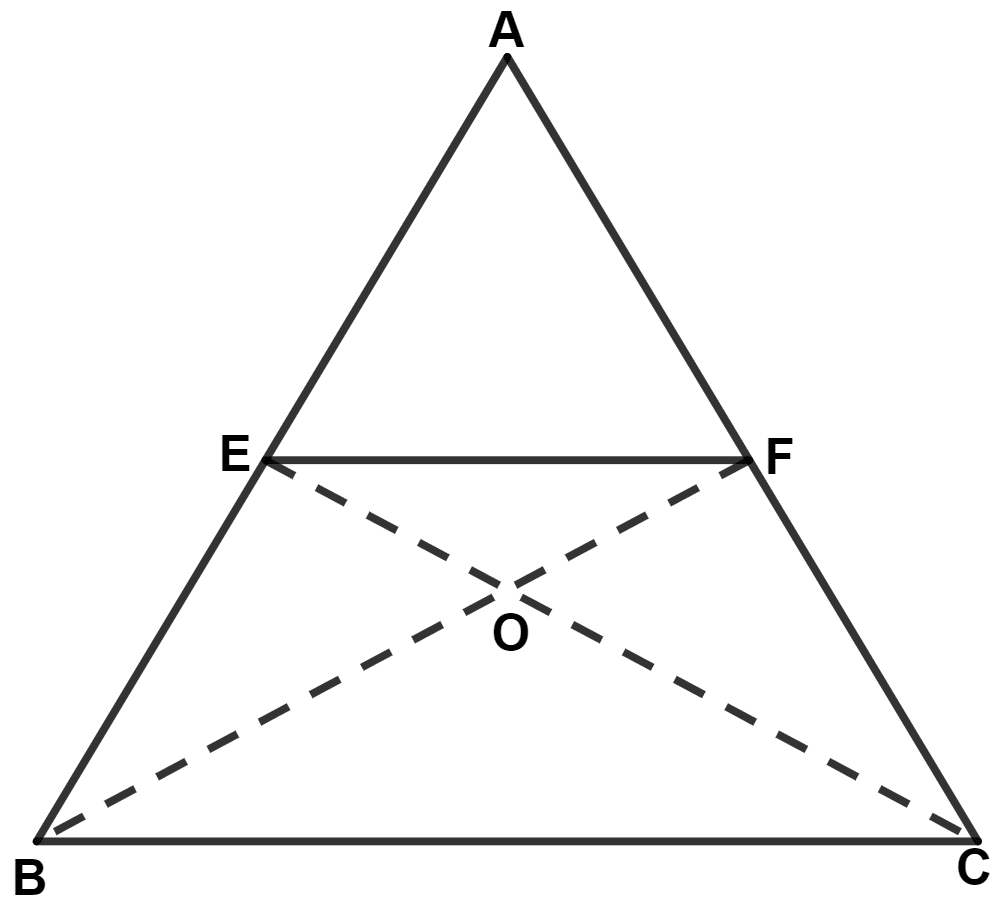
In △ ABC,
Since, E and F are mid-points of sides AB and AC respectively.
∴ EF || BC.
We know that,
The areas of two triangles lying on same base and between same parallel lines are equal.
From figure,
△ BEF and △ CEF lie on same base EF and between same parallel lines EF and BC.
∴ Area of △ BEF = Area of △ CEF
⇒ Area of △ BEF - Area of △ EOF = Area of △ CEF - Area of △ EOF
⇒ Area of △ BOE = Area of △ COF …….(1)
Since, F is the mid-point of AC.
∴ BF is the median of triangle.
We know that,
Median of triangle divides the triangle into two triangles of equal area.
∴ Area of △ ABF = Area of △ CBF
⇒ Area of △ ABF - Area of △ BOE = Area of △ CBF - Area of △ BOE
⇒ Area of △ ABF - Area of △ BOE = Area of △ CBF - Area of △ COF [From equation (1)]
⇒ Area of quadrilateral AEOF = Area of △ OBC.
Hence, proved that △ OBC and quadrilateral AEOF are equal in area.
Related Questions
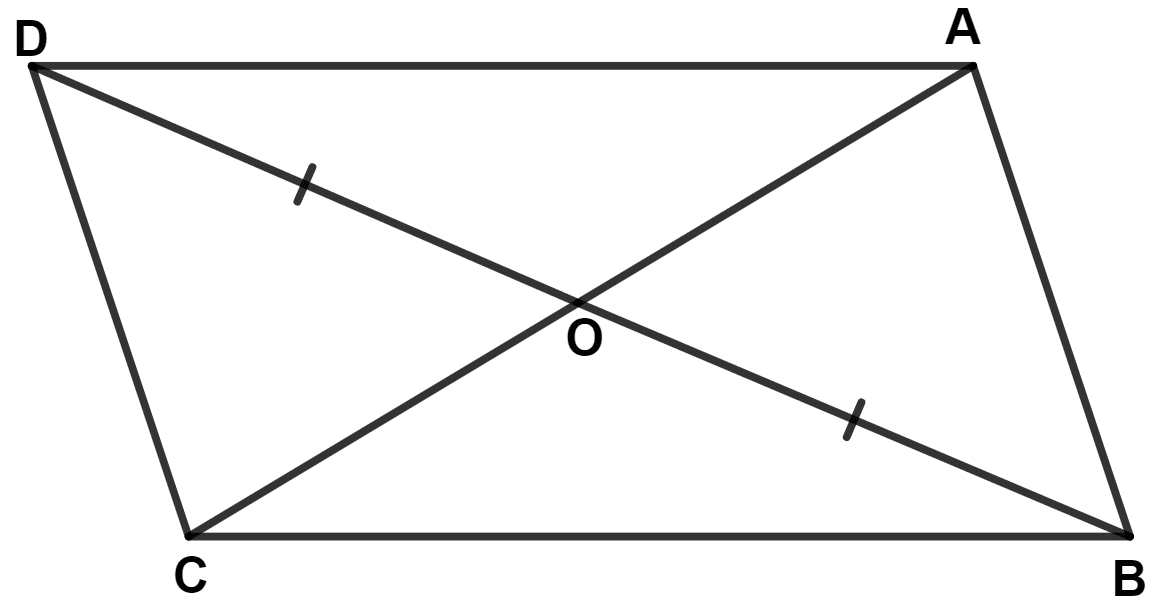
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB // DC, prove that :
(i) Area of (△ DOC) = Area of (△ AOB)
(ii) Area of (△ DCB) = Area of (△ ACB)
(iii) ABCD is a parallelogram.
The given figure shows a parallelogram ABCD with area 324 sq.cm. P is a point in AB such that AP : PB = 1 : 2. Find the area of △ APD.
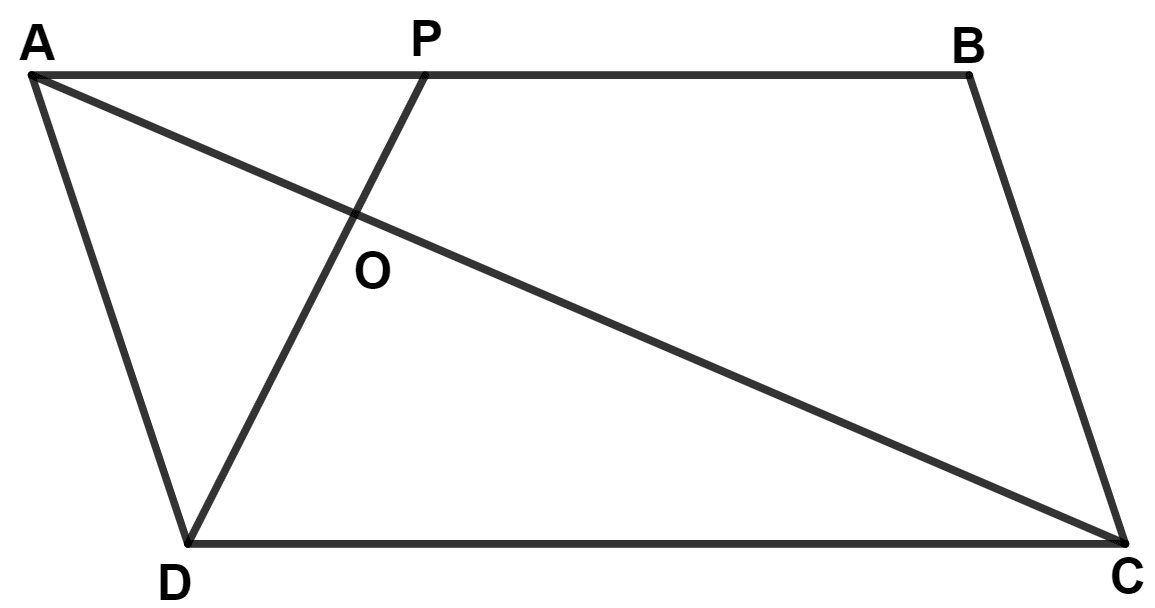
In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of △ POB = 40 cm2 and OP : OC = 1 : 2, find :
(i) Areas of △ BOC and △ PBC
(ii) Area of △ ABC and parallelogram ABCD.