In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of △ POB = 40 cm² and OP : OC = 1 : 2, find :

(i) Areas of △ BOC and △ PBC

(ii) Area of △ ABC and parallelogram ABCD.

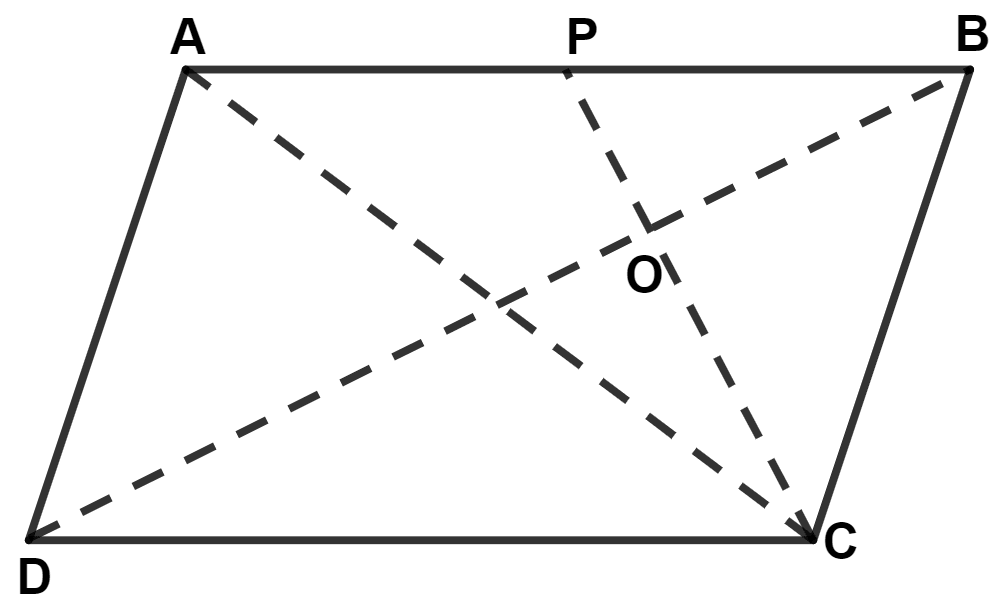
(i) Given,

OP : OC = 1 : 2

We know that,

Ratio of the area of triangles with same vertex and bases along the same line is equal to the ratio of their respective bases.

$\Rightarrow \dfrac{\text{Area of △ POB}}{\text{Area of △ BOC}} = \dfrac{OP}{OC} \\[1em] \Rightarrow \dfrac{40}{\text{Area of △ BOC}} = \dfrac{1}{2} \\[1em] \Rightarrow \text{Area of △ BOC} = 2 \times 40 = 80 \text{ cm}^2.$

From figure,

Area of △ PBC = Area of △ BOC + Area of △ POB = 80 + 40 = 120 cm².

Hence, area of △ BOC = 80 cm² and area of △ PBC = 120 cm².

(ii) Given,

P is the mid-point of AB.

∴ CP is the median of △ ABC.

We know that,

Median of triangle divides it into two triangles of equal area.

∴ Area of △ APC = Area of △ PBC = 120 cm².

From figure,

⇒ Area of △ ABC = Area of △ APC + Area of △ BPC = 120 + 120 = 240 cm².

We know that,

The area of triangle is half that of a parallelogram on the same base and between the same parallels.

Since, △ ABC and || gm ABCD lies on same base AB and between same parallel lines AB and DC.

∴ Area of △ ABC = $\dfrac{1}{2}$ Area of || gm ABCD

⇒ Area of || gm ABCD = 2 Area of △ ABC = 2 × 240 = 480 cm².

Hence, area of △ ABC = 240 cm² and || gm ABCD = 480 cm².