Mathematics
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6 : 5 : 4. Find the lengths of its sides.
Theorems on Area
10 Likes
Answer
Let the sides be x cm, y cm and (37 - x - y) cm. Also, the length of altitudes be 6a, 5a and 4a cm.
By formula,
Area of triangle = base × height
Area of triangle ABC =
Solving L.H.S. of the equation :
Solving L.H.S. of the equation :
Substituting value of x from equation (1) in above equation, we get :
Substituting value of y in equation (1), we get :
Sides : x = 10 cm, y = 12 cm, (37 - x - y) = (37 - 10 - 12) = 15 cm.
Hence, sides of triangle ABC are 10 cm, 12 cm and 15 cm.
Answered By
3 Likes
Related Questions
In parallelogram ABCD, P is mid-point of AB. CP and BD intersect each other at point O. If area of △ POB = 40 cm2 and OP : OC = 1 : 2, find :
(i) Areas of △ BOC and △ PBC
(ii) Area of △ ABC and parallelogram ABCD.
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD, prove that :
(i) Area (△ ABD) = 3 × Area (△ BGD)
(ii) Area (△ ACD) = 3 × Area (△ CGD)
(iii) Area (△ BGC) = × Area (△ ABC)
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF : FE = 5 : 3 and area of △ ADF is 60 cm2; find :
(i) area of △ ADE
(ii) if AE : EB = 4 : 5, find the area of △ ADB.
(iii) also, find area of parallelogram ABCD.
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = CA.
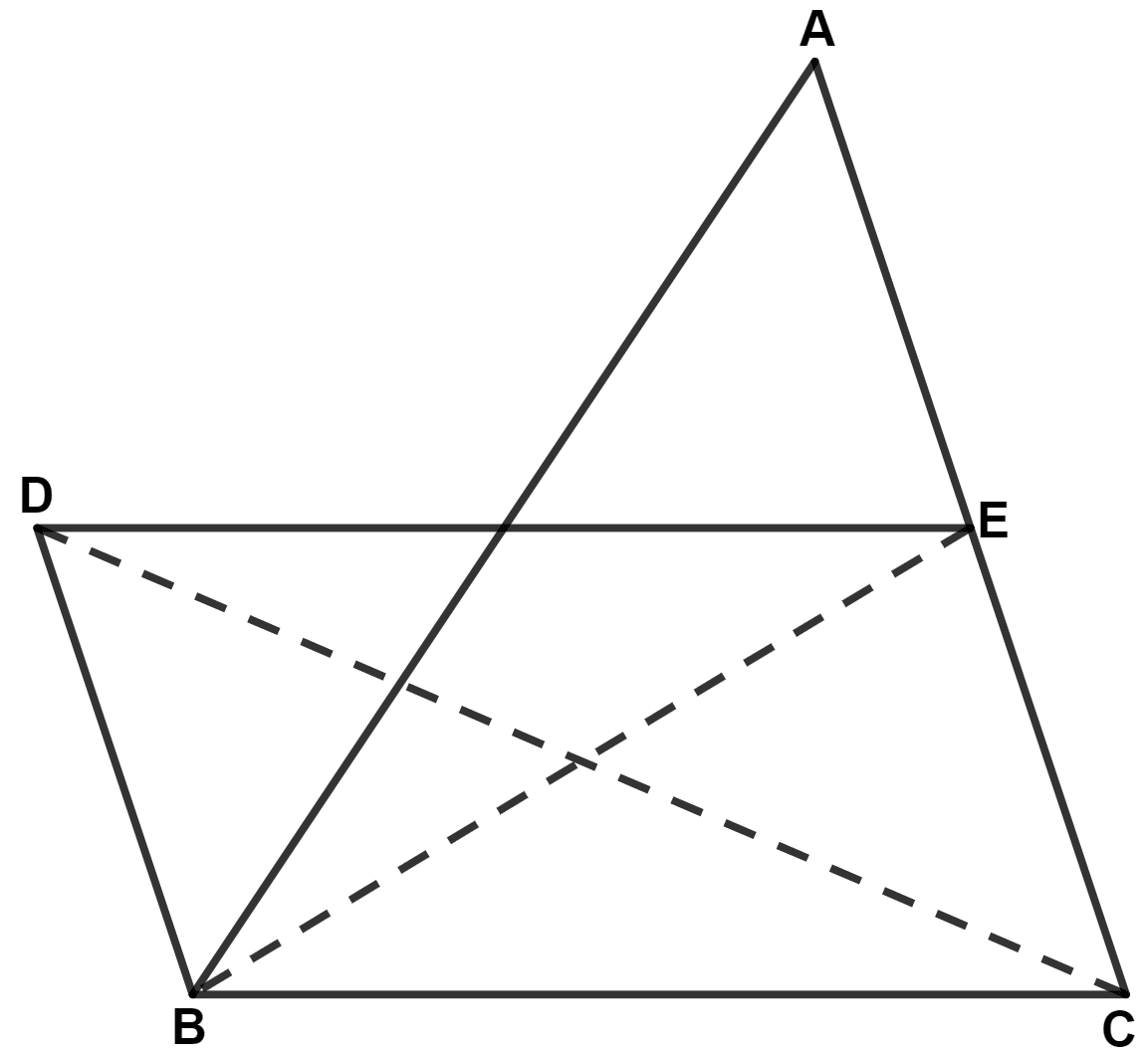
Prove that : ar.(△ ABC) = 2 × ar.(△ DBC)