Mathematics
Answer
ABCD is an isosceles trapezium in which AD = BC.
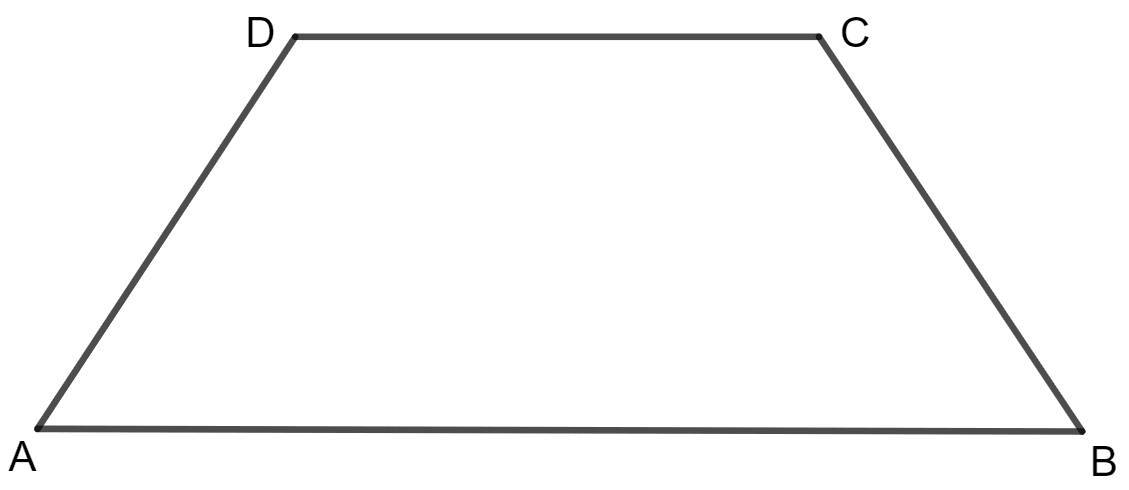
To prove:
∠ A + ∠ C = 180°
and, ∠ B + ∠ D = 180°
Proof:
AB is parallel to CD. So, sum of adjacent angles is 180°.
⇒ ∠ A + ∠ D = 180°
It is already given that ABCD is an isosceles trapezium which means AD = BC.
⇒ ∠ A = ∠ B
So,
⇒ ∠ B + ∠ D = 180°
In a trapezium, sum of all angles is always equal to 360°.
⇒ ∠ A + ∠ B + ∠ C + ∠ D = 360°
⇒ ∠ A + ∠ C + (∠ B + ∠ D) = 360°
⇒ ∠ A + ∠ C + 180° = 360°
⇒ ∠ A + ∠ C = 360° - 180°
⇒ ∠ A + ∠ C = 180°
Hence, the opposite angles are supplementary.
Related Questions
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30°, find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
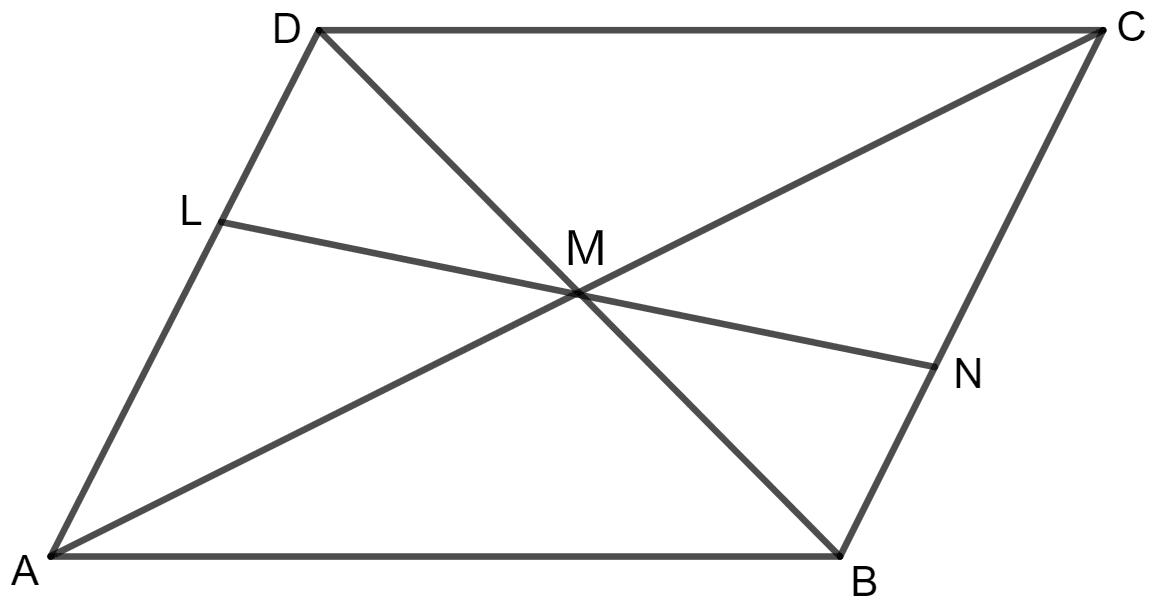
Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is the mid-point of LN.
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD ?
(ii) AC is perpendicular to BD but is not equal to it ?
(iii) AC = BD but AC is not perpendicular to BD?
Prove that the diagonals of a parallelogram bisect each other.