Mathematics
Prove that the diagonals of a parallelogram bisect each other.
Quadrilaterals
7 Likes
Answer
Given:
ABCD is an parallelogram.
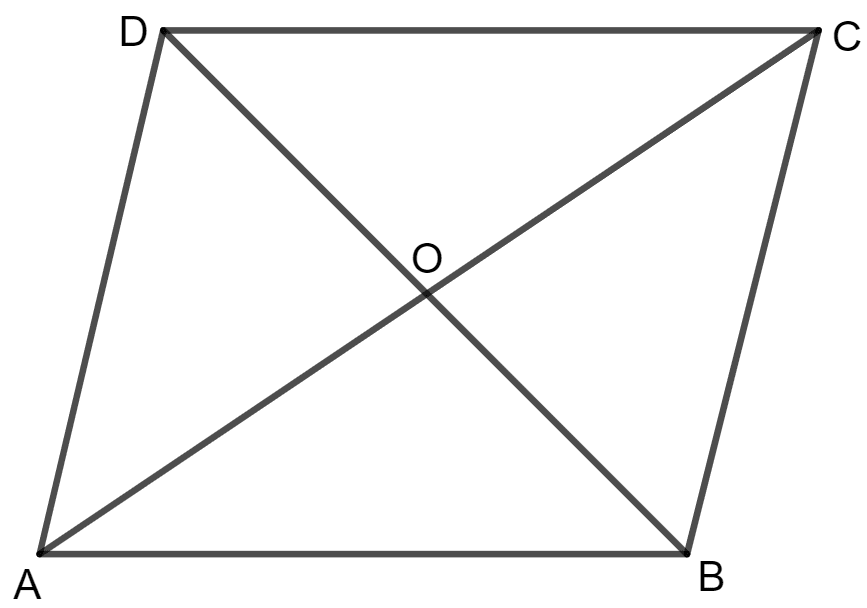
To prove:
OA = OC and OB = OD
Proof:
As ABCD is a parallelogram which means AB is parallel to CD.
In Δ OCD and Δ OAB
∠ OBA = ∠ ODC (alternate angles)
∠ OAB = ∠ OCD (alternate angles)
AB = CD (opposite side of parallelogram)
By Angle side angle congruency
Δ OCD ≅ Δ OAB
By using Corresponding parts of congruent triangles,
OA = OC and OB = OD
Hence, the diagonals of a parallelogram bisect each other.
Answered By
5 Likes
Related Questions
In an isosceles-trapezium, show that the opposite angles are supplementary.
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD ?
(ii) AC is perpendicular to BD but is not equal to it ?
(iii) AC = BD but AC is not perpendicular to BD?
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.