Mathematics
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Quadrilaterals
10 Likes
Answer
Given:
Parallelogram ABCD in which E and F are mid - points of AD and BC.
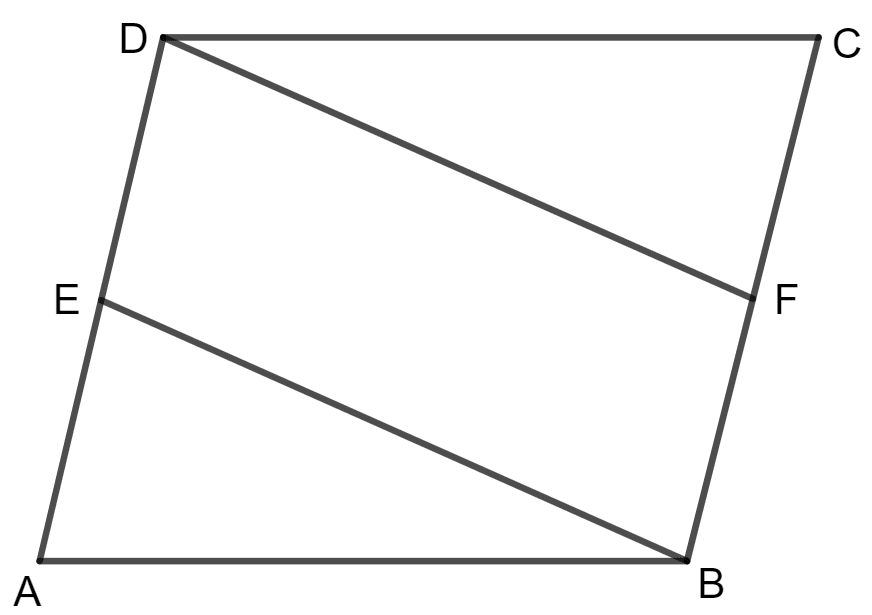
To prove:
BFDE is a parallelogram
Proof:
E is the mid-point of AD.
DE = AD
Also, F is the mid-point of BC.
BF = BC
But as we know opposite sides of parallelogram are equal.
So, AD = BC
Therefore, DE = BF
And, also AD is parallel to BC.
So, DE is parallel to BF.
When DE = BF and DE is parallel to BF. (opposite sides are equal and parallel to each other)
Hence, BFDE is a parallelogram.
Answered By
8 Likes
Related Questions
Prove that the diagonals of a parallelogram bisect each other.
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
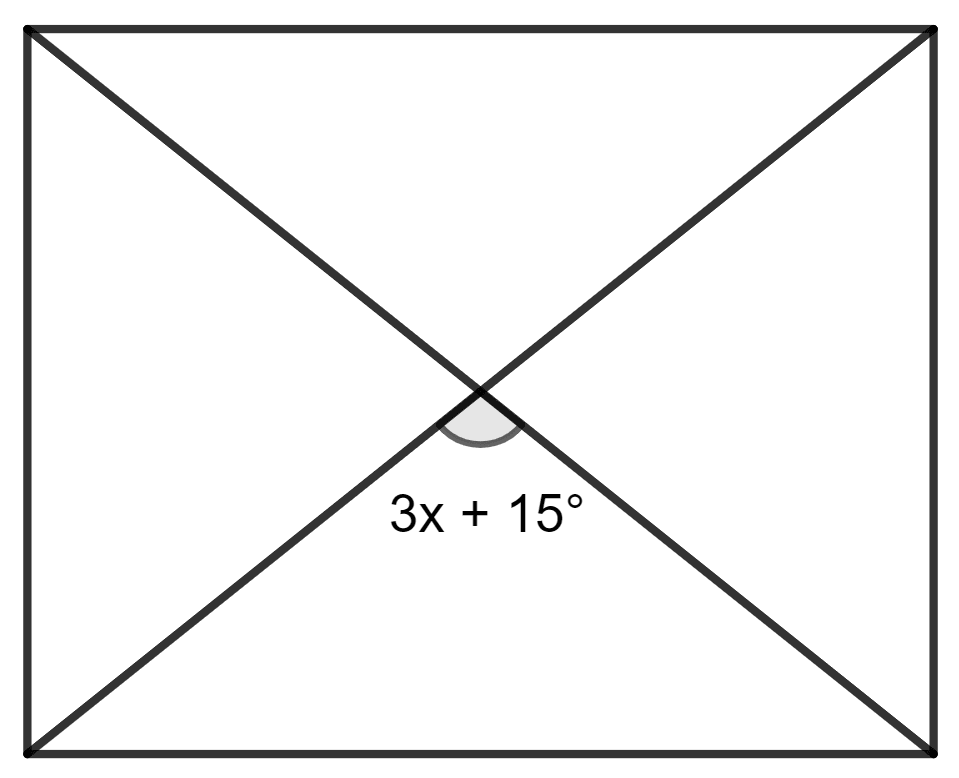
The given figure shows a parallelogram. The value of x for which it will be a rhombus is :
35°
25°
15°
45°
A rhombus will be a square, if :
its diagonals bisect each other
its diagonals are perpendicular to each other
one of its angles is 60°
none of these