Mathematics
In isosceles triangle ABC, AB = AC. The side BA is produced to D such that BA = AD. Prove that : ∠BCD = 90°.
Related Questions
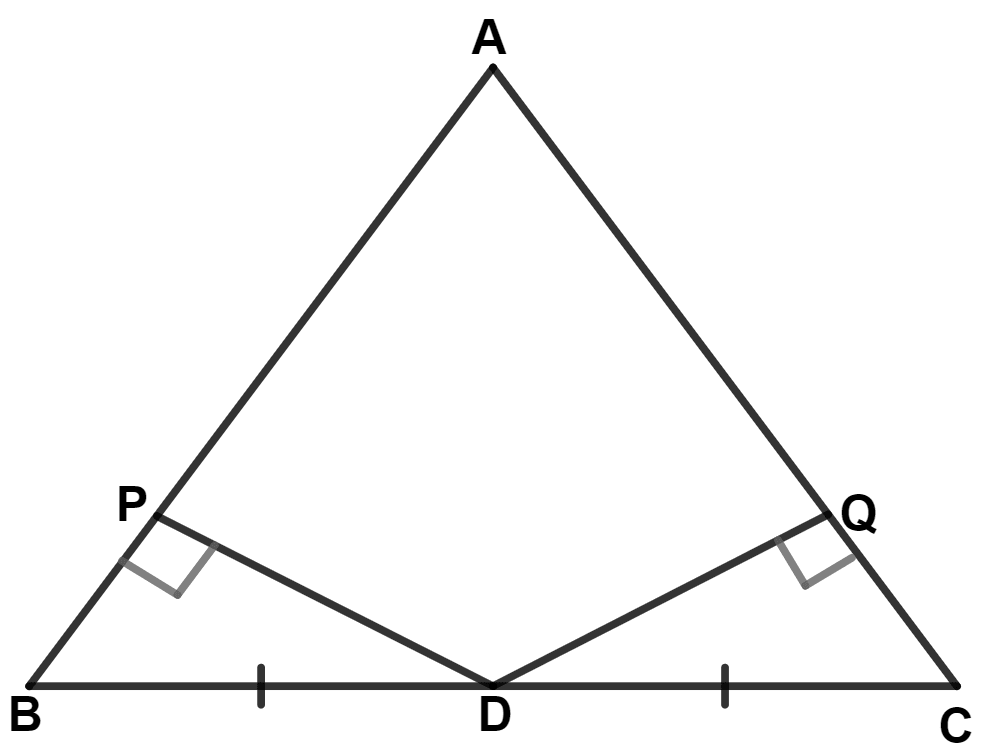
In the given figure, AB = AC. Prove that :
(i) DP = DQ
(ii) AP = AQ
(iii) AD bisects angle A
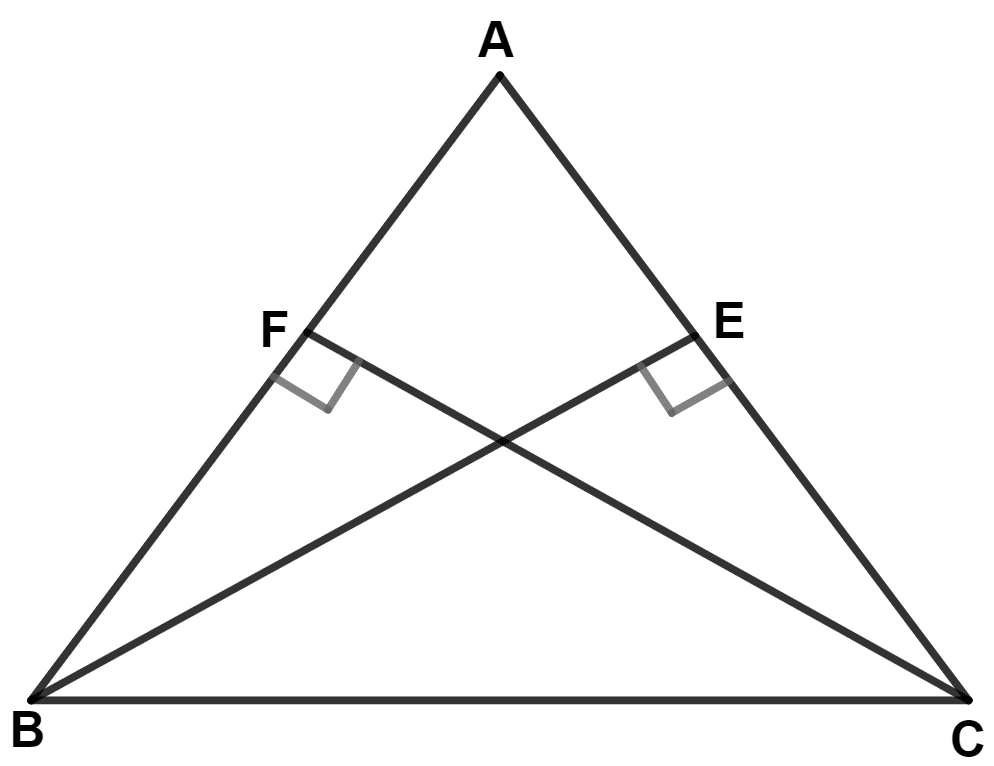
In triangle ABC, AB = AC; BE ⊥ AC and CF ⊥ AB. Prove that :
(i) BE = CF
(ii) AF = AE
In a triangle ABC, AB = AC and ∠A = 36°. If the internal bisector of ∠C meets AB at point D, prove that AD = BC.
If the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.