In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x - 7 and CD = 3x + 1, find the length of CD.

It is given that in parallelogram ABCD, ∠A = 3 times ∠B.

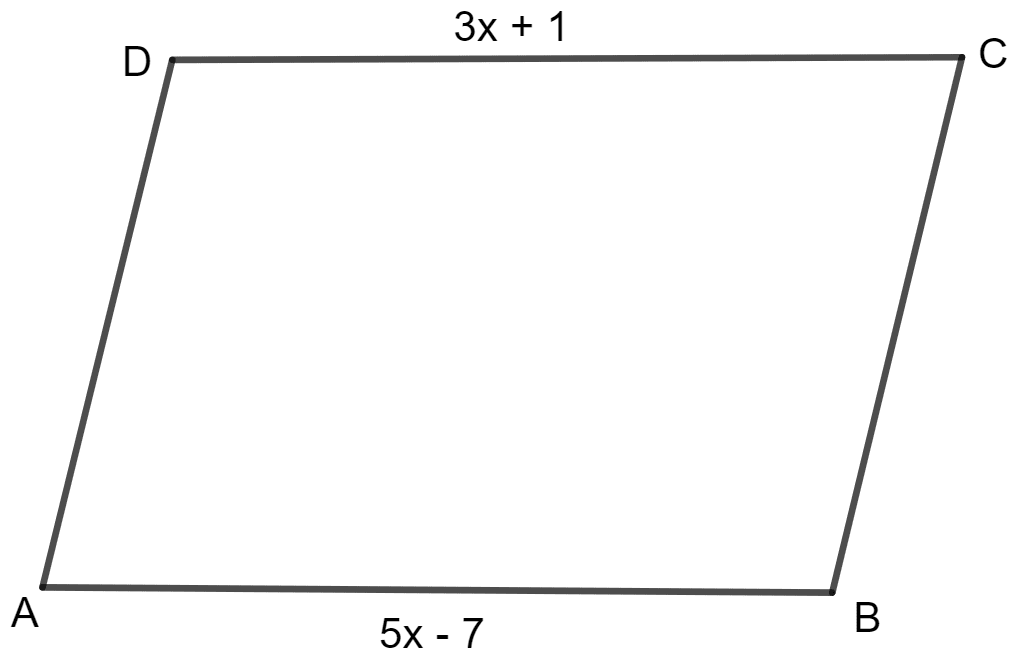
Let ∠B be a.

Then, ∠A = 3a.

As we know, the consecutive angles of a parallelogram are supplementary.

⇒ ∠A + ∠B = 180°

⇒ 3a + a = 180°

⇒ 4a = 180°

⇒ a = $\dfrac{180°}{4}$

⇒ a = 45°

Thus, ∠B = ∠D = a = 45°.

And, ∠A = ∠C = 3a = 3 $\times$ 45° = 135°

It is also given that AB = 5x - 7 and CD = 3x + 1.

AB = CD (opposite sides of parallelogram are equal)

⇒ (5x - 7) = (3x + 1)

⇒ 5x - 7 = 3x + 1

⇒ 5x - 3x = 7 + 1

⇒ 2x = 8

⇒ x = $\dfrac{8}{2}$

⇒ x = 4

CD = 3x + 1

= 3 $\times$ 4 + 1

= 12 + 1

= 13

Hence, ∠A = 135°, ∠C = 135°, ∠B = 45°, ∠D = 45° and CD = 13 units.