Mathematics
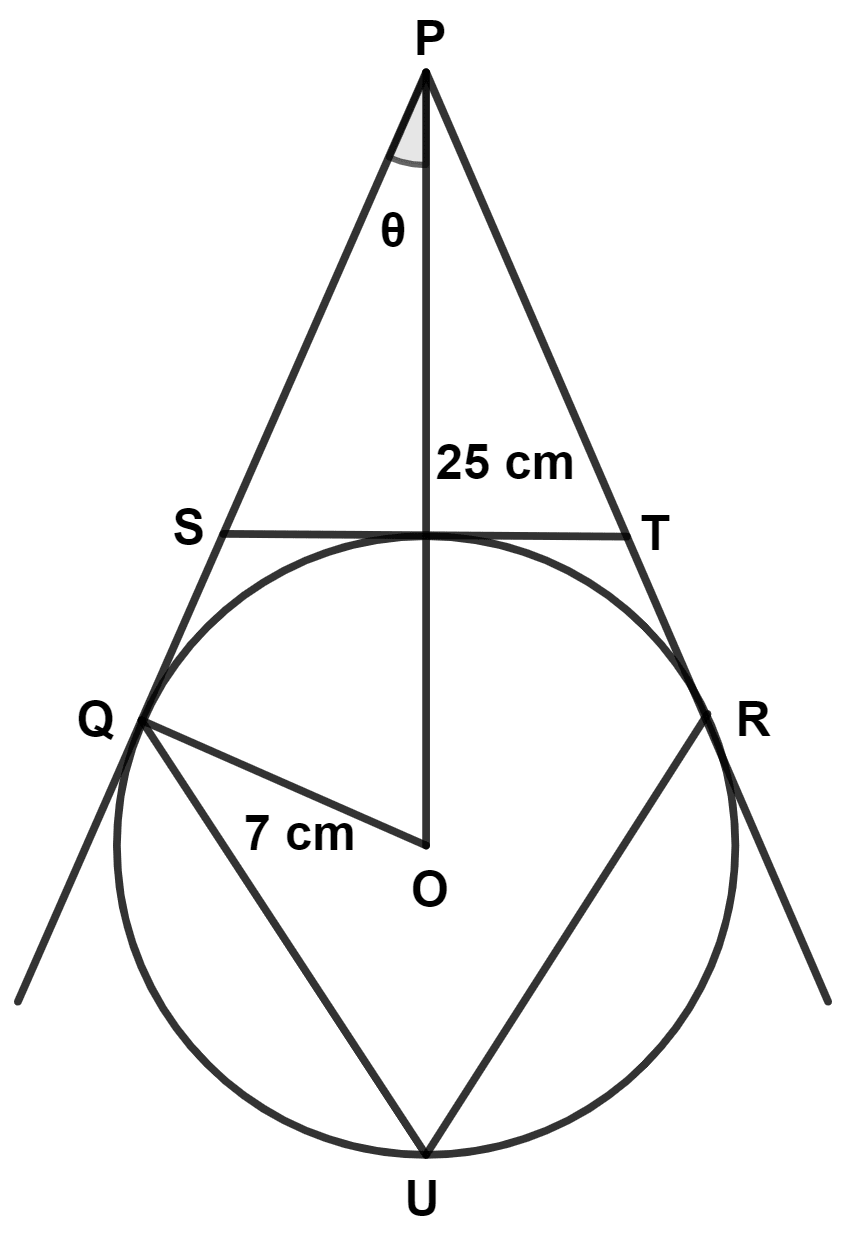
In the adjoining diagram PQ, PR and ST are the tangents to the circle with centre O and radius 7 cm. Given OP = 25 cm. Find :
(a) length of ST
(b) value of ∠OPQ, i.e. θ
(c) ∠QUR, in nearest degree
Circles
67 Likes
Answer
(a) We know that,
The radius of a circle and tangent are perpendicular at the point of contact.
∴ ∠PQO = 90°
In right-angled triangle PQO,
⇒ PO2 = PQ2 + OQ2
⇒ 252 = PQ2 + 72
⇒ 625 = PQ2 + 49
⇒ PQ2 = 625 - 49
⇒ PQ2 = 576
⇒ PQ = = 24 cm.
In △ POQ,
⇒ tan θ =
⇒ tan θ = ……………(1)
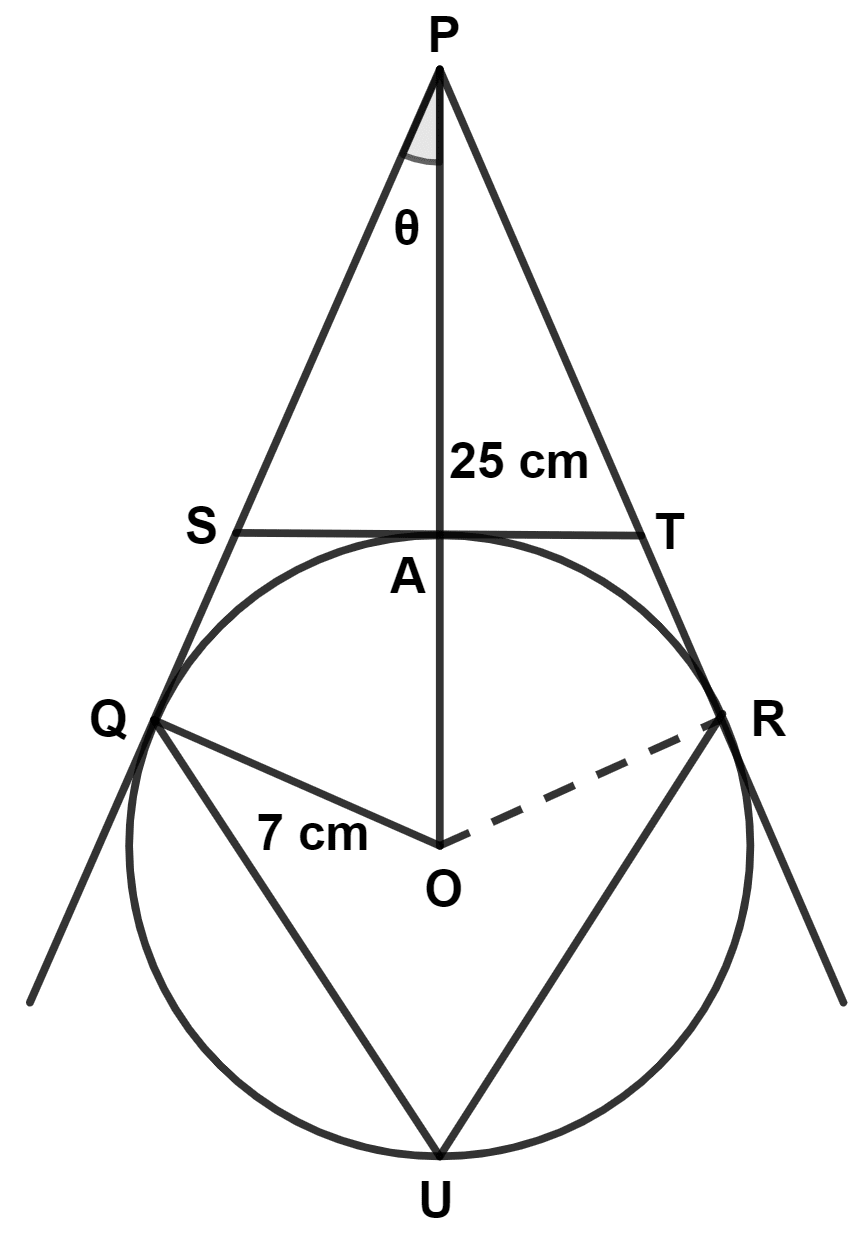
From figure,
⇒ ∠PAS = 90°
⇒ PA = OP - OA = 25 - 7 = 18 cm.
⇒ tan θ =
⇒ tan θ = ………..(2)
From equation (1) and (2), we get :
From figure,
⇒ ST = 2 × AS = = 10.5 cm
Hence, ST = 10.5 cm.
(b) From equation (1),
⇒ tan θ =
⇒ tan θ = 0.292
⇒ tan θ = tan 16° 16'
⇒ θ = 16° 16'.
Hence, θ = 16° 16'.
(c) In △ POQ,
⇒ ∠POQ + ∠PQO + ∠QPO = 180°
⇒ ∠POQ + 90° + 16° 16' = 180°
⇒ ∠POQ + 106° 16' = 180°
⇒ ∠POQ = 180° - 106° 16' = 73° 44' = 74°.
We know that,
Tangent from an external point to the circle are equal in length.
∴ PQ = PR.
Also,
OR = OQ (Both equal to radius of circle)
In △ POQ and △ POR,
⇒ PQ = PR (Proved above)
⇒ OQ = OR (Radius of same circle)
⇒ PO = PO (Common side)
∴ △ POQ ≅ △ POR (By S.S.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ ∠POR = ∠POQ = 74°
From figure,
⇒ ∠QOR = ∠POR + ∠POQ = 74° + 74° = 148°.
We know that,
The angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference.
⇒ ∠QOR = 2∠QUR
⇒ ∠QUR = = 74°.
Hence, ∠QUR = 74°.
Answered By
28 Likes
Related Questions
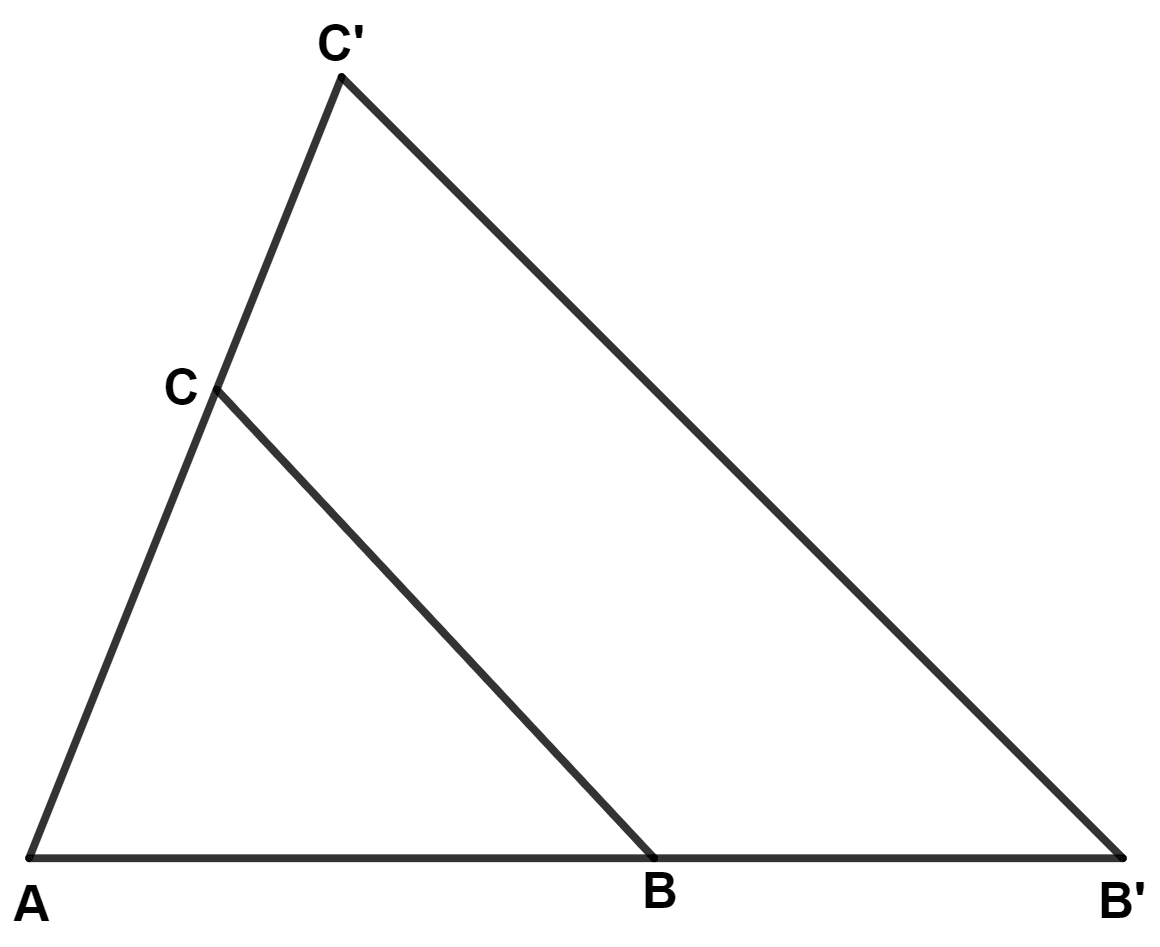
While preparing a PowerPoint presentation, ∆ ABC is enlarged along the side BC to ∆ AB'C', as shown in the diagram, such that BC ∶ B'C' is 3 ∶ 5. Find :
(a) AB ∶ BB'
(b) length AB, if BB' = 4 cm.
(c) Is ∆ ABC ~ ∆ AB'C' ? Justify your answer.
(d) ar (∆ ABC) : ar (quad. BB'C'C).
The approximate volume of a human eye is 6.5 cm3. The volume of a laboratory model (excluding base and stand) of the human eye is 1404 cm3.

(a) State whether the scale factor k is less than, equals to or greater than 1.
(b) Calculate the:
(i) value of k
(ii) diameter of the human eye if the radius of the model is 7.2 cm.
(iii) the external surface area of the human eye if the surface area of the model is 651.6 cm2.
Use ruler and compass to answer this question. Construct a triangle ABC where AB = 5.5 cm, BC = 4.5 cm and angle ABC = 135°. Construct the circumcircle to the triangle ABC. Measure and write down the length of AC.
The curved surface area of a right circular cone is half of another right circular cone. If the ratio of their slant heights is 2 : 1 and that of their volumes is 3 : 1, find ratio of their:
(a) radii
(b) heights