Mathematics
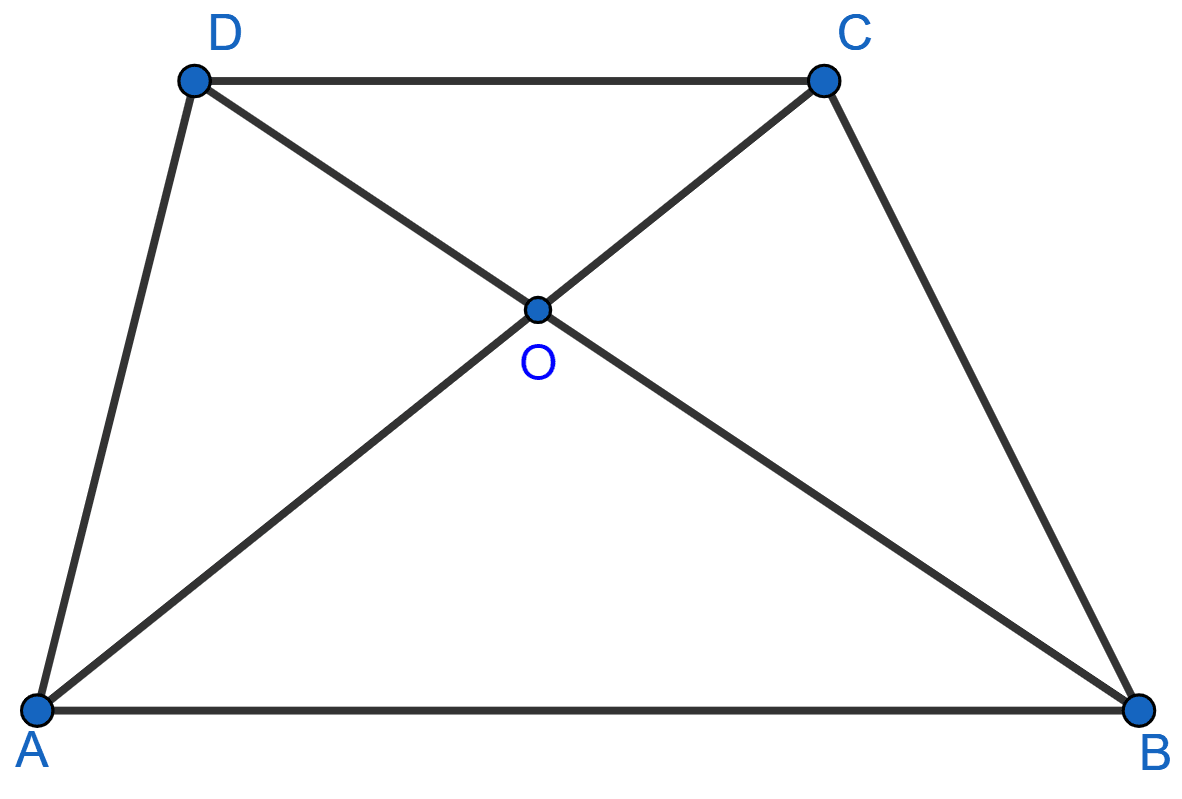
In the adjoining figure, AB || DC and AB ≠ DC. If the diagonals AC and BD of the trapezium ABCD intersect at O, then which of the following statements is not true ?
area of △ABC = area of △ABD
area of △ACD = area of △BCD
area of △OAB = area of △OCD
area of △OAD = area of △OBC
Answer
We know that,
Triangles on the same base and between same parallel lines are equal in area.
Hence,
⇒ area of △ABC = area of △ABD …….. (1)
⇒ area of △ACD = area of △BCD
From figure and eqn. (1),
area of (△AOB + △OAD) = area of (△AOB + △OBC)
⇒ area of △OAD = area of △OBC.
Hence, Option 3 is the correct option.
Related Questions
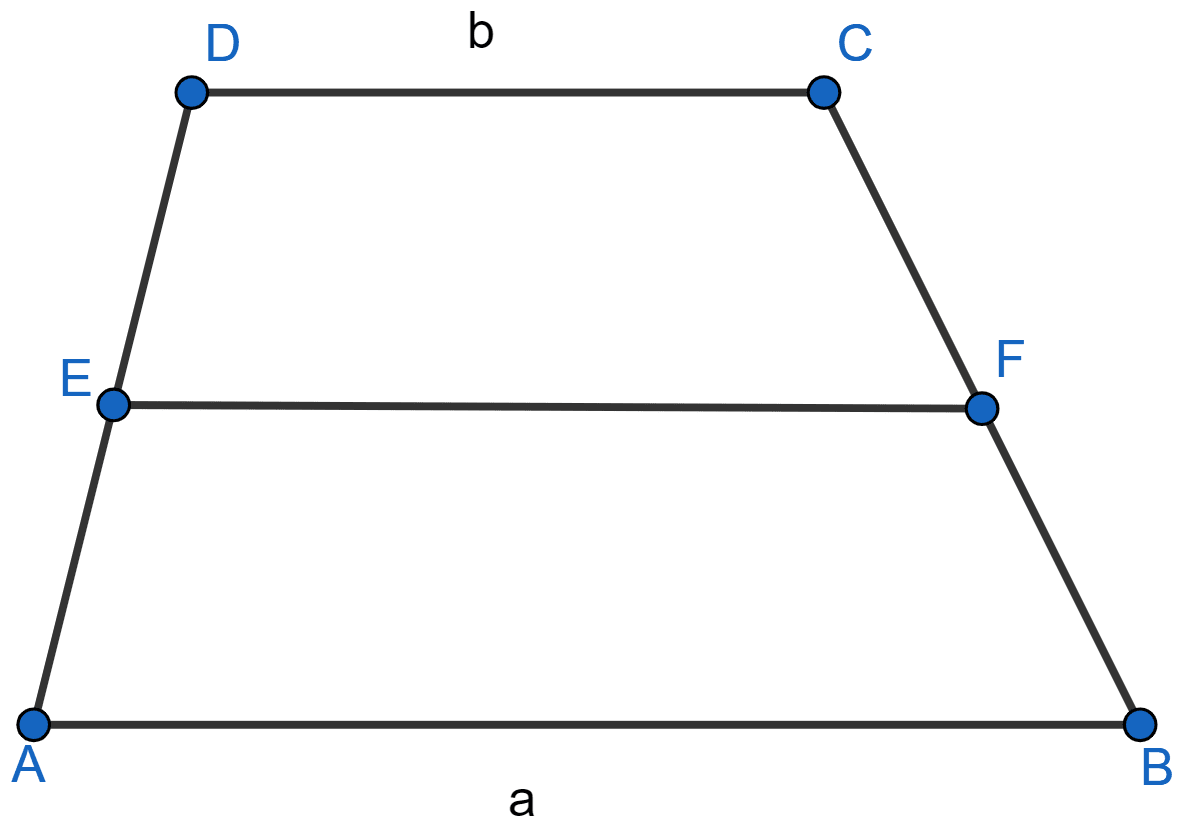
In the adjoining figure, ABCD is a trapezium with parallel sides AB = a cm and DC = b cm. E and F are mid-points of the non-parallel sides. The ratio of area of ABFE and area of EFCD is
a : b
(3a + b) : (a + 3b)
(a + 3b) : (3a + b)
(2a + b) : (3a + b)
Consider the following two statements:
Statement 1: The line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
Statement 2: Diagonals of a parallelogram divide it into four triangles of equal area.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.