Mathematics
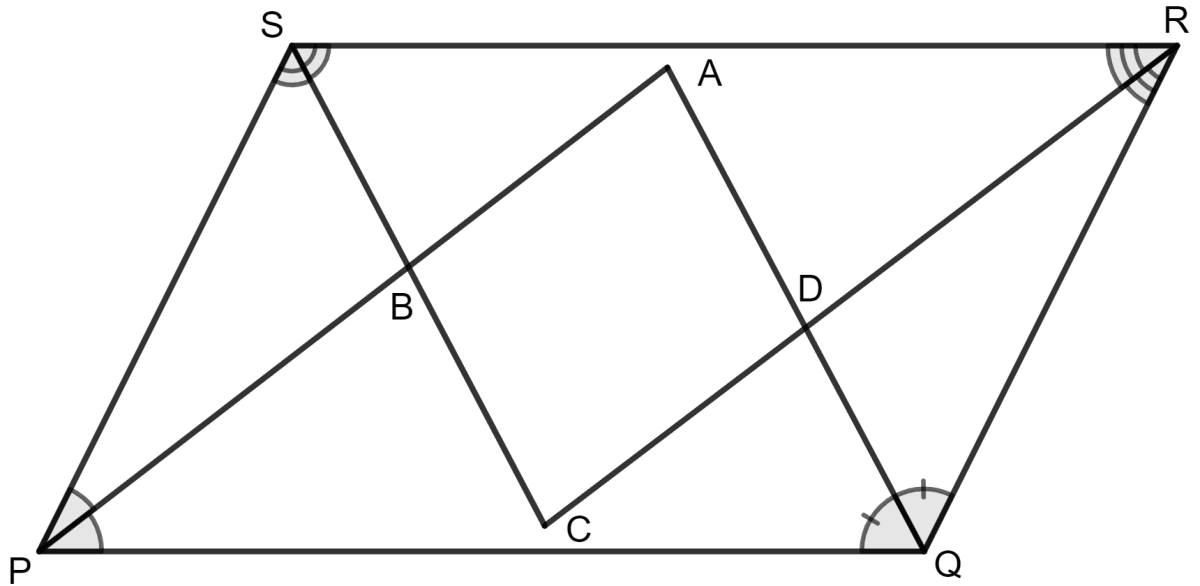
In the diagram given below, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD. Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Quadrilaterals
14 Likes
Answer
(i) Given:
PQRS is a parallelogram.
To prove:
∠PSB + ∠SPB = 90°
Proof:
It is given that AP and CS is an angle bisectors.
∠SPB = ∠BPQ and ∠PSB = ∠BSR
As PS is parallel to QR,
⇒ ∠SPQ + ∠PSR = 180°
⇒ (∠SPQ + ∠PSR) = 180°
⇒ ∠SPQ + ∠PSR = 90°
⇒ ∠SPB + ∠PSB= 90°
Hence, ∠PSB + ∠SPB = 90°.
(ii) To prove:
∠PBS = 90°
Proof:
In triangle PBS, the sum of all the angles is 180°.
⇒ ∠PSB + ∠SPB + ∠PBS = 180°
Using ∠PSB + ∠SPB = 90°, we get
⇒ 90° + ∠PBS = 180°
⇒ ∠PBS = 180° - 90°
⇒ ∠PBS = 90°
Hence, ∠PBS = 90°.
(iii)To prove:
∠ABC = 90°
Proof:
∠PBS = ∠ABC (vertically opposite angles)
∠PBS = 90°
So, ∠ABC = 90°
Hence, ∠ABC = 90°.
(iv) To prove:
∠ADC = 90°
Proof:
PQRS is a parallelogram.
As PS is parallel to QR,
⇒ ∠SRQ + ∠RQP = 180°
⇒ (∠SRQ + ∠RQP) = 180°
⇒ ∠SRQ + ∠RQP = 90°
⇒ ∠DRQ + ∠RQD = 90°
In triangle RDQ, the sum of all the angles is 180°.
⇒ ∠DRQ + ∠DQR + ∠QDR = 180°
Using ∠DRQ + ∠RQD = 90°, we get
⇒ 90° + ∠QDR = 180°
⇒ ∠QDR = 180° - 90°
⇒ ∠QDR = 90°
∠QDR = ∠ADC (vertically opposite angles)
So, ∠ADC = 90°
Hence, ∠ADC = 90°.
(v) To prove:
∠A = 90°
Proof:
In triangle APQ, the sum of all the angles is 180°.
⇒ ∠APQ + ∠AQP + ∠PAQ = 180°
⇒ (∠APQ + ∠AQP) + ∠PAQ = 180°
[∵ ∠ APQ = ∠ SPQ and ∠ AQP = ∠ RQP ]
As we know opposite side of parallelogram are equal.
So, ∠ RQP = ∠ PSR
Therefore, ∠ AQP = ∠ PSR
⇒ (∠SPQ + ∠PSR) + ∠PAQ = 180°
⇒ 90° + ∠PAQ = 180°
⇒ ∠PAQ = 180° - 90°
⇒ ∠PAQ = 90°
Hence, ∠A = 90°.
(vi) To prove:
ABCD is a rectangle.
Proof:
∠A = ∠B = ∠D = 90°
Sum of each angle of quadrilateral is 360°.
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 90° + 90° + ∠C + 90° = 360°
⇒ 270° + ∠C = 360°
⇒ ∠C = 360° - 270°
⇒ ∠C = 90°
Each angle of the quadrilateral is 90°.
Hence, ABCD is a rectangle.
Answered By
9 Likes
Related Questions
One of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.
In a parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD
(ii) DE bisects ∠ADC and
(iii) Angle DEC is a right angle.
In a parallelogram ABCD, X and Y are mid-points of opposite sides AB and DC respectively. Prove that:
(i) AX = YC.
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
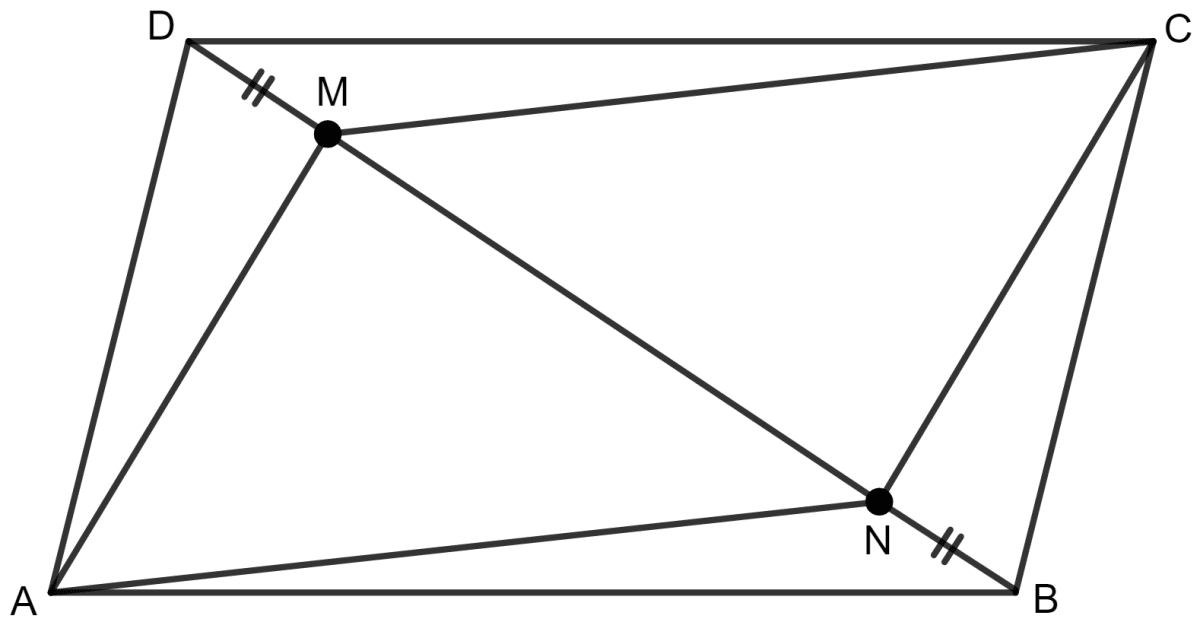
The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN. Prove that:
(i) △DMC ≅ △BNA and so CM = AN.
(ii) △AMD ≅ △CNB and so AM = CN.
(iii) ANCM is a parallelogram.