Mathematics
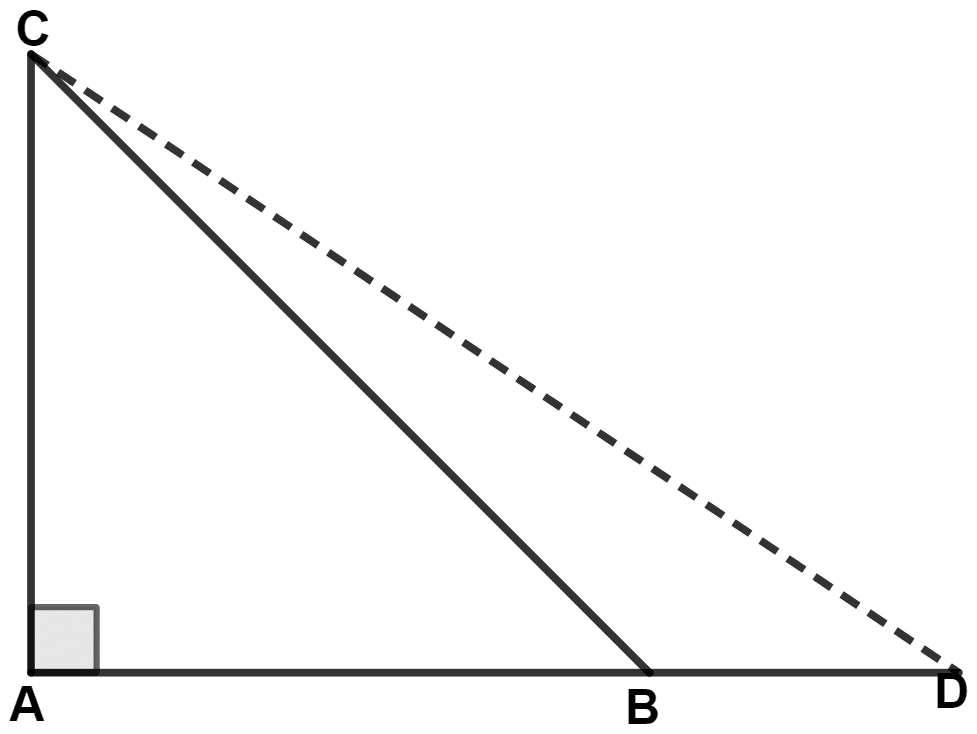
In the figure, AB = BC and AD is perpendicular to CD. Prove that :
AC2 = 2.BC.DC.
Pythagoras Theorem
11 Likes
Answer
By formula,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + Base2
In right angle triangle ABD,
By pythagoras theorem,
⇒ AB2 = AD2 + BD2
⇒ AD2 = AB2 - BD2 ………(1)
In right angle triangle ACD,
By pythagoras theorem,
⇒ AC2 = AD2 + DC2
= (AB2 - BD2) + (DB + BC)2 [From equation (1)]
= AB2 - BD2 + DB2 + BC2 + 2.DB.BC
= AB2 + BC2 + 2.DB.BC
= BC2 + BC2 + 2.DB.BC [As, AB = BC]
= 2BC2 + 2.DB.BC
= 2BC(BC + DB)
= 2BC.DC
Hence, proved that AC2 = 2BC.DC
Answered By
5 Likes
Related Questions
In the given figure, diagonals AC and BD intersect at right angle. Show that :
AB2 + CD2 = AD2 + BC2
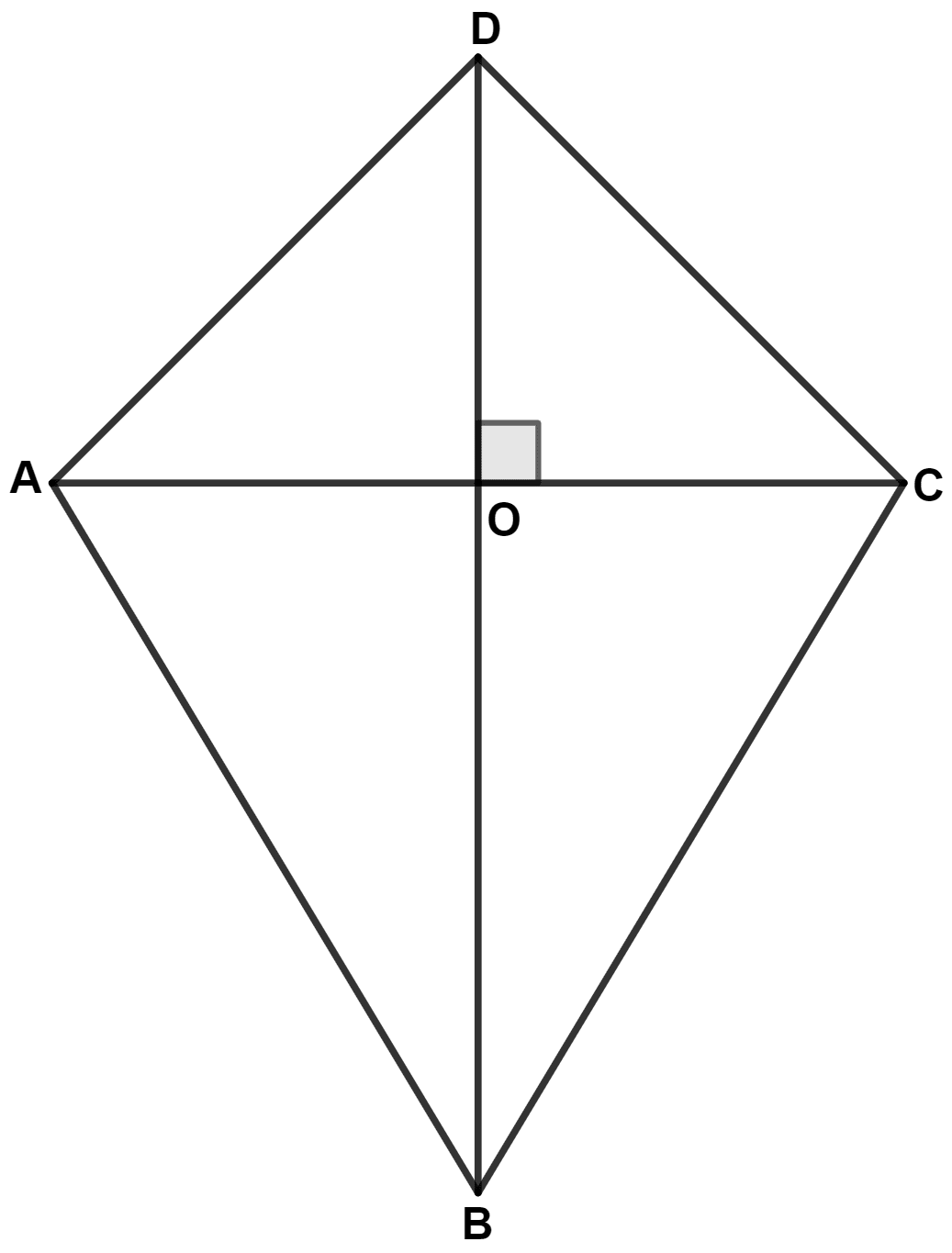
Diagonals of rhombus ABCD intersect each other at point O. Prove that :
OA2 + OC2 = 2AD2 -
In an isosceles triangle ABC; AB = AC and D is a point on BC produced. Prove that :
AD2 = AC2 + BD.CD
In triangle ABC, angle A = 90°, CA = AB and D is a point on AB produced. Prove that :
DC2 - BD2 = 2AB.AD.