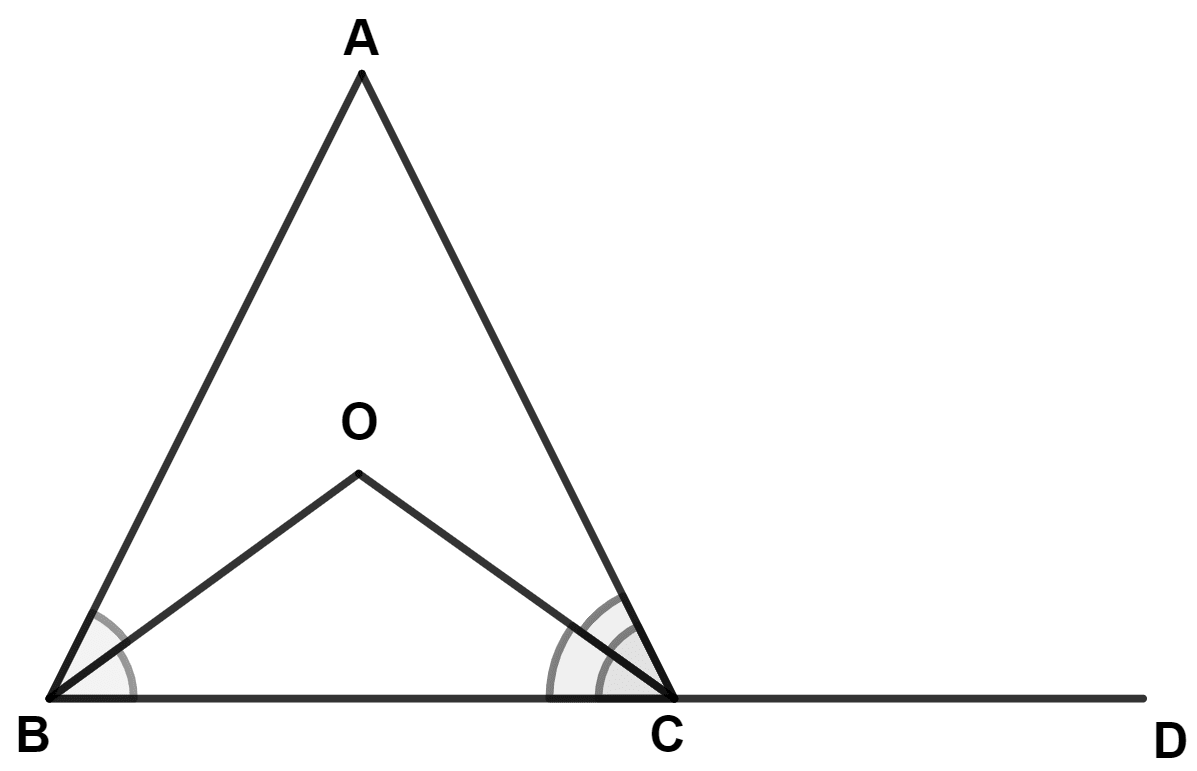
In the figure, given below, AB = AC. Prove that : ∠BOC = ∠ACD.

In △ ABC,

⇒ AB = AC (Given)

∴ ∠C = ∠B = x (let)

From figure,

OB and OC bisects angle ∠B and ∠C.

∴ ∠OBC = $\dfrac{∠B}{2} = \dfrac{x}{2}$ and ∠OCB = $\dfrac{∠C}{2} = \dfrac{x}{2}$.

In △ BOC,

By angle sum property of triangle,

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ $\dfrac{x}{2} + \dfrac{x}{2}$ + ∠BOC = 180°

⇒ x + ∠BOC = 180°

⇒ ∠BOC = 180° - x.

From figure,

⇒ ∠OCA = $\dfrac{x}{2}$ (As OC is bisector of ∠C)

Since, BCD is a straight line.

∴ ∠OCB + ∠OCA + ∠ACD = 180°

⇒ $\dfrac{x}{2} + \dfrac{x}{2}$ + ∠ACD = 180°

⇒ x + ∠ACD = 180°

⇒ ∠ACD = 180° - x.

∴ ∠BOC = ∠ACD.

Hence, proved that ∠BOC = ∠ACD.