Mathematics
In the figure (ii) given below, O and O' are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that,
(i) M bisects AB.
(ii) ∠APB = 90°.

Related Questions
In the figure (ii) given below, two circles with centres C, C' intersect at A, B and the point C lies on the circle with C'. PQ is a tangent to the circle with centre C' at A. Prove that AC bisects ∠PAB.

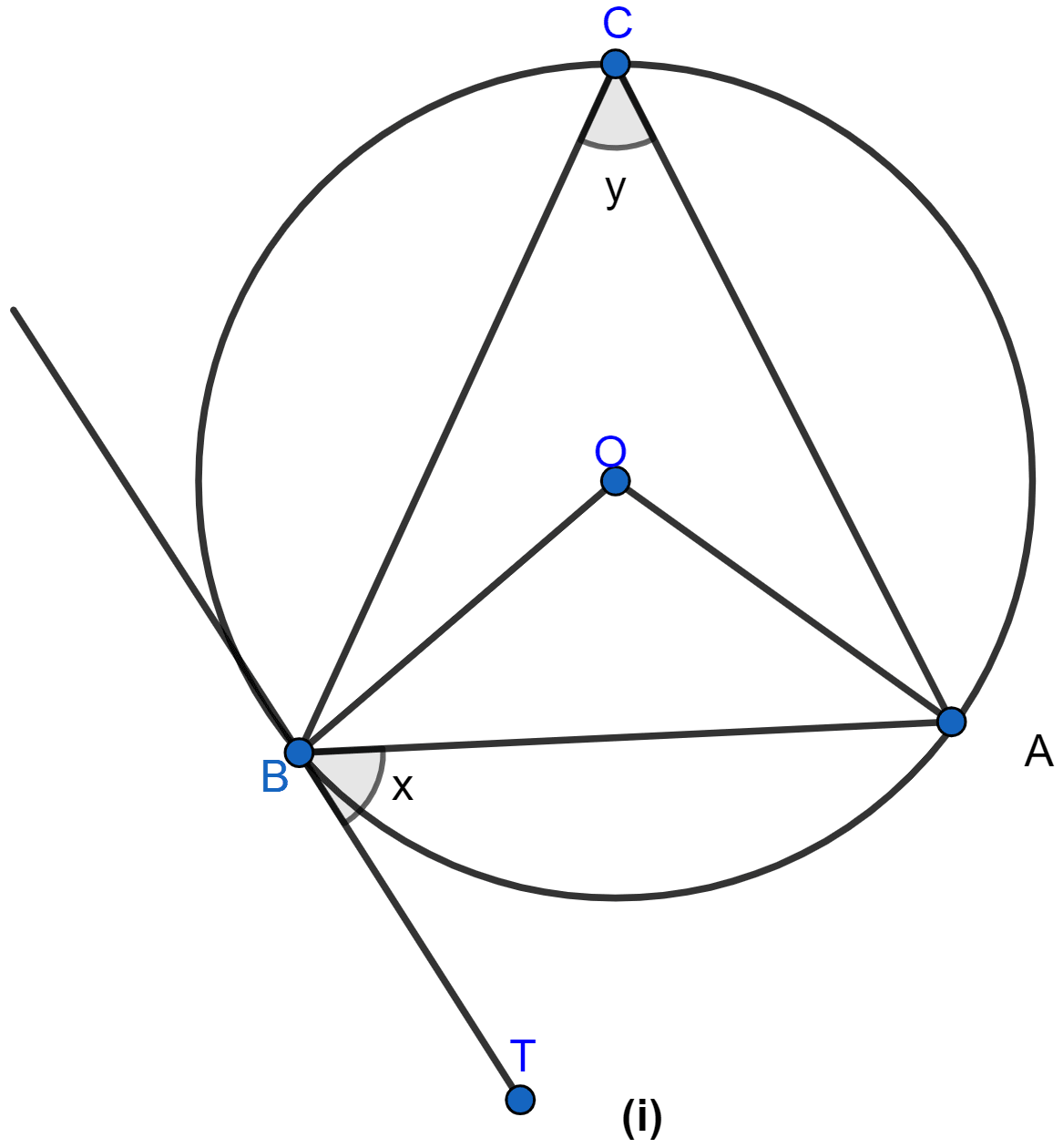
In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.
In adjoining figure, P and Q are the centers of two circles touching externally at R and CD is the common tangent.
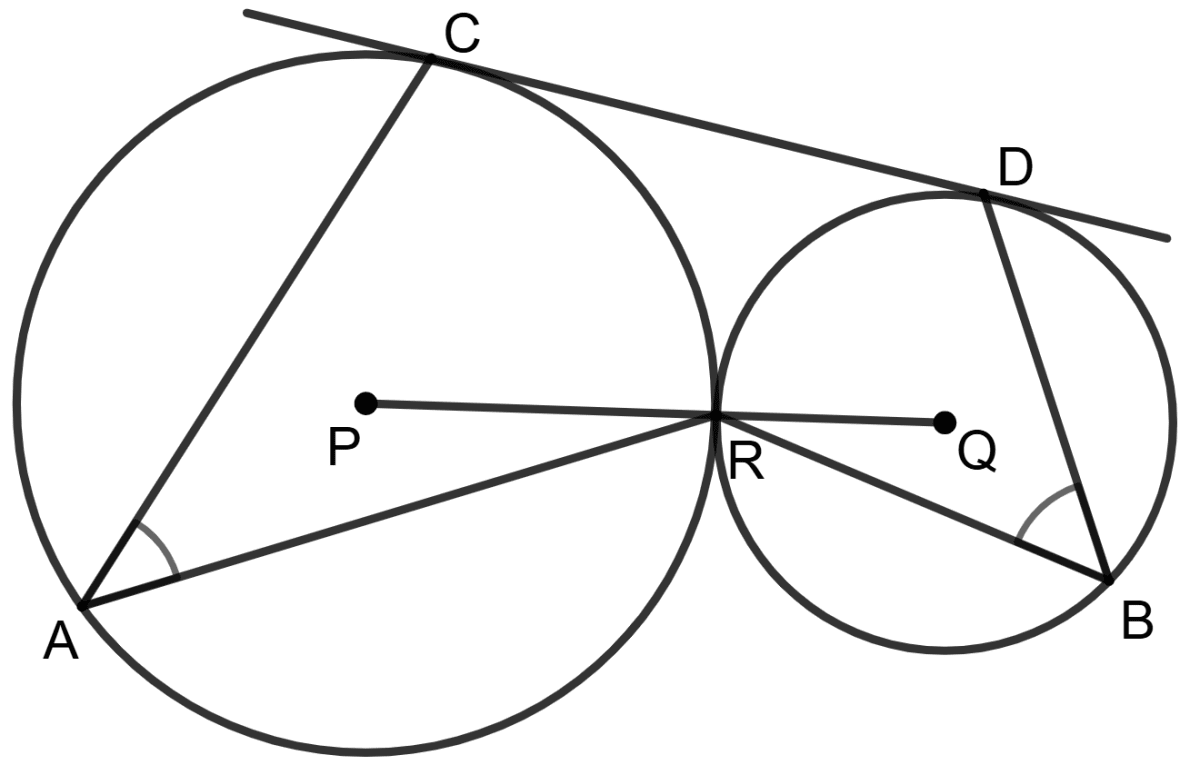
If ∠CAR = 38°, then find ∠DBR.
In the adjoining figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to
50°
40°
60°
70°
