Mathematics
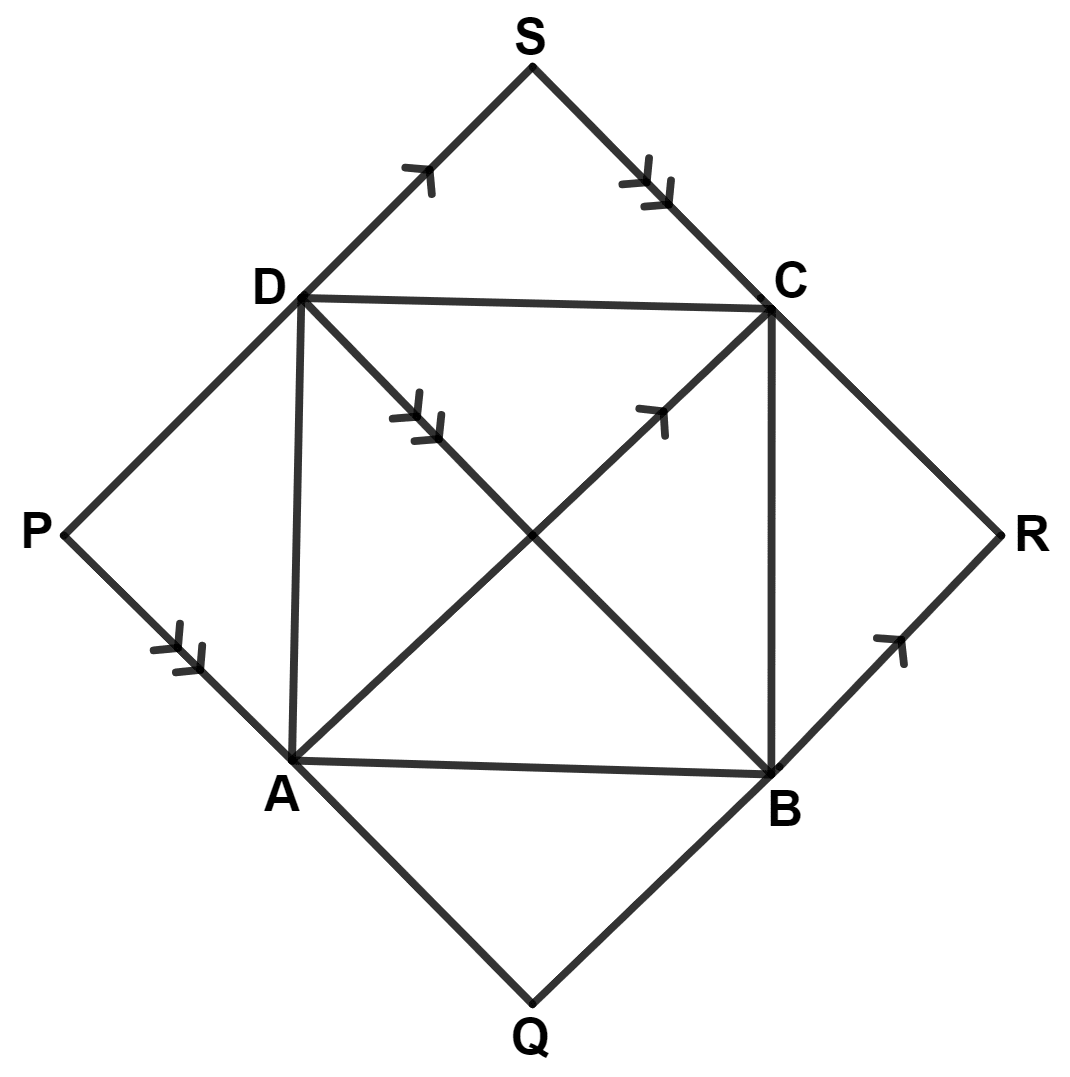
In the following figure, AC // PS // QR and PQ // DB // SR.
Prove that :
Area of quadrilateral PQRS = 2 × Area of quad.ABCD.
Theorems on Area
6 Likes
Answer
From figure,
PQRS is a parallelogram.
Given,
AC // PS // QR and PQ // DB // SR.
∴ AQRC and APSC are also parallelograms.
We know that,
The area of a triangle is half that of a parallelogram on the same base and between the same parallels.
From figure,
△ ABC and || gm AQRC lie on same base AC and between same parallel lines AC and QR.
∴ Area of △ ABC = Area of || gm AQRC …………(1)
△ ADC and || gm ACSP lie on same base AC and between same parallel lines AC and PS.
∴ Area of △ ADC = Area of || gm ACSP …………(2)
Adding equations (1) and (2), we get :
⇒ Area of △ ABC + Area of △ ADC = Area of || gm AQRC + Area of || gm ACSP
⇒ Area of quadrilateral ABCD = (Area of || gm AQRC + Area of || gm ACSP)
⇒ Area of quadrilateral ABCD = Area of || PQRS
⇒ Area of || gm PQRS = 2 × Area of quadrilateral ABCD.
Hence, proved that area of quadrilateral PQRS = 2 × area of quad. ABCD.
Answered By
3 Likes
Related Questions
ABCD and BCFE are parallelograms. If area of triangle EBC = 480 cm2, AB = 30 cm and BC = 40 cm; Calculate :
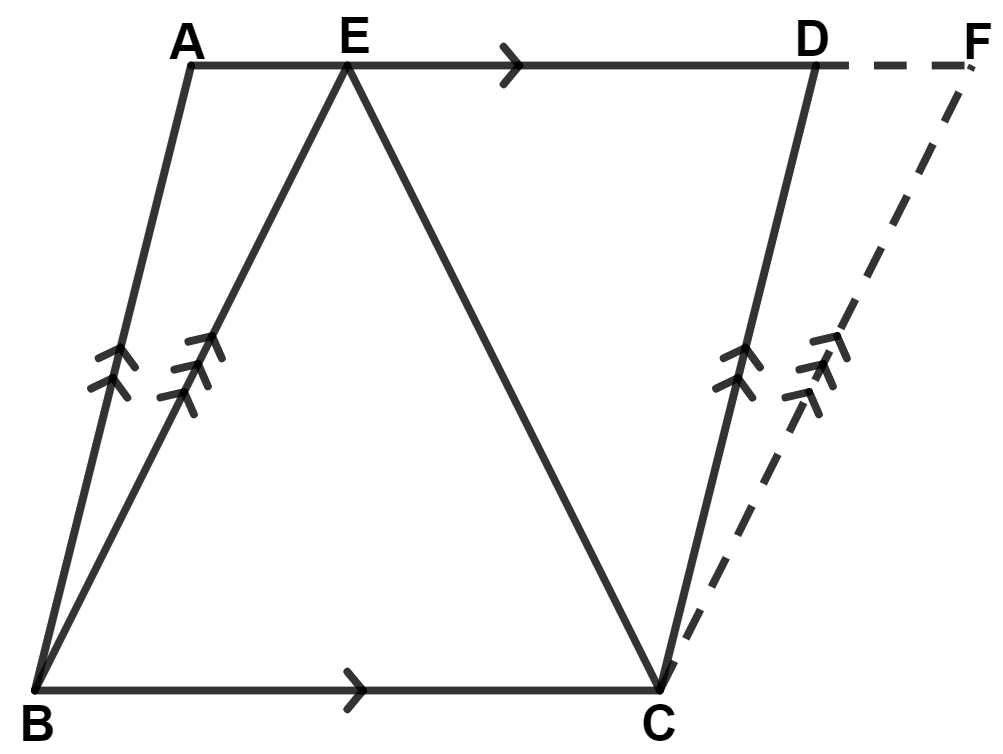
(i) area of parallelogram ABCD;
(ii) area of the parallelogram BCFE;
(iii) length of altitude from A on CD;
(iv) area of triangle ECF.
In the given figure, D is mid-point of side AB of △ ABC and BDEC is a parallelogram.
Prove that :
Area of △ ABC = Area of // gm BDEC.
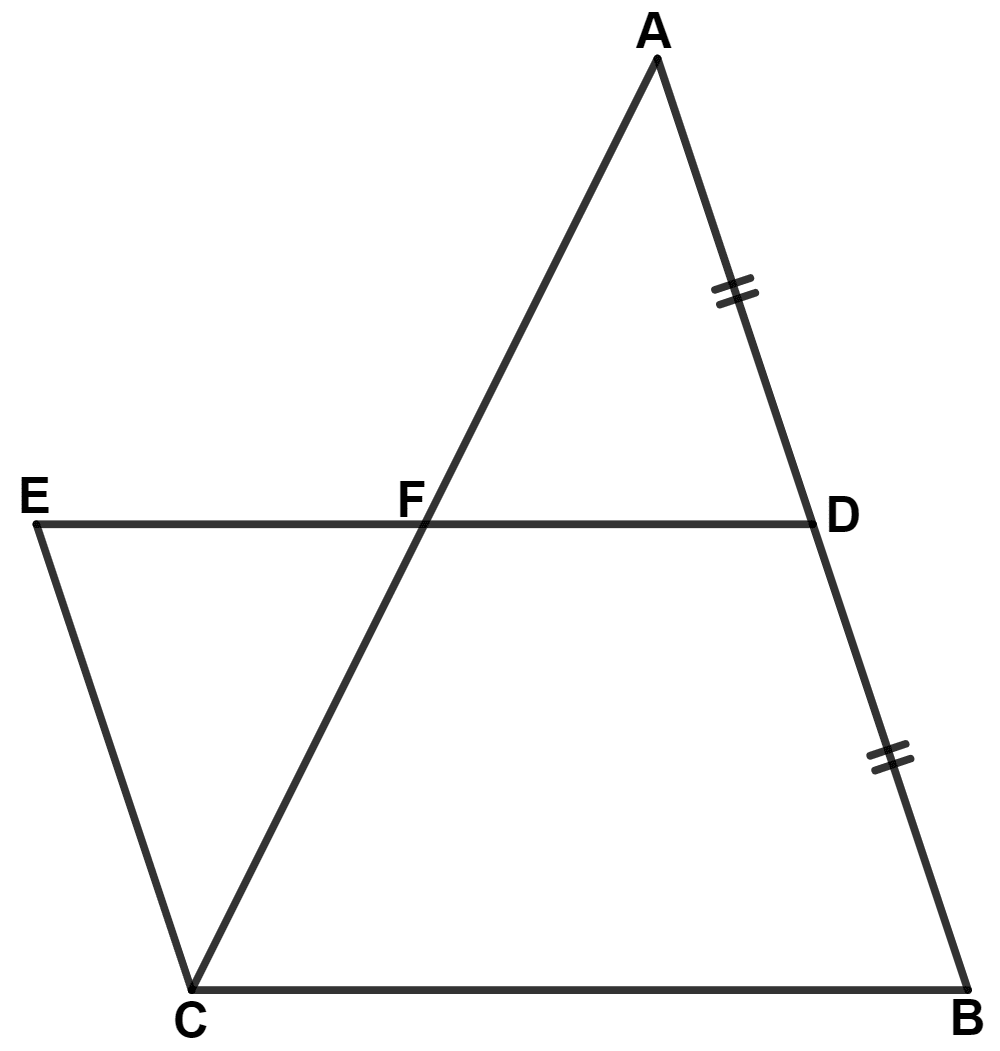
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that :
area of △ ADM = area of △ ACN.
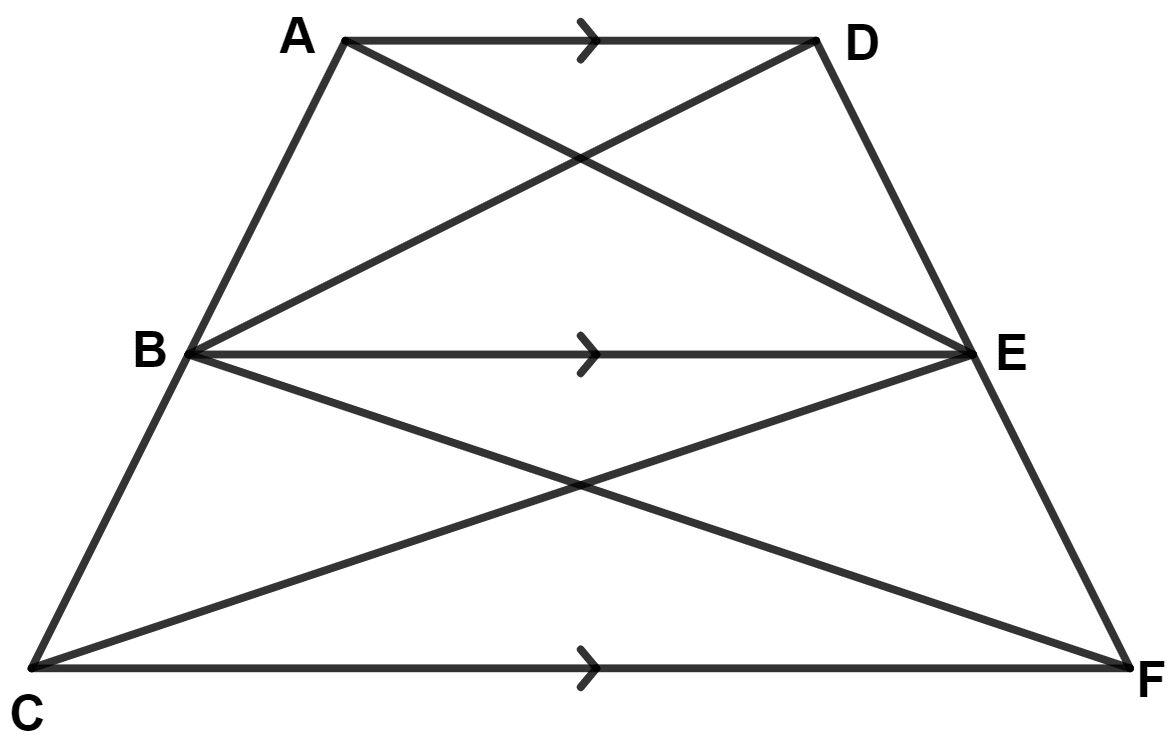
In the given figure, AD // BE // CF. Prove that :
area (△ AEC) = area (△ DBF)