Mathematics
In the following figure, BD is parallel to CA, E is mid-point of CA and BD = 1/2 CA. Prove that : ar.(△ ABC) = 2 × ar.(△ DBC)
Answer
Since,
⇒ BD || CA
∴ BD || CE
Also,
BD = CE.
Since, BD = CE and BD || CE,
∴ BCED is a parallelogram.
We know that,
The area of triangle on same base and between the same parallels are equal in area.
△ DBC and △ EBC lie on the same base BC and between same parallel lines BC and ED.
∴ Area of △ DBC = Area of △ EBC …………(1)
In △ ABC,
E is the mid-point of AC.
∴ BE is the median of triangle.
∴ Area of △ EBC = Area of △ ABE ……….(2)
From figure,
⇒ Area of △ ABC = Area of △ EBC + Area of △ ABE
⇒ Area of △ ABC = Area of △ EBC + Area of △ EBC [From equation (2)]
⇒ Area of △ ABC = 2 Area of △ EBC
⇒ Area of △ ABC = 2 Area of △ DBC. [From equation (1)]
Hence, proved that area of △ ABC = 2 area of △ DBC.
Related Questions
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6 : 5 : 4. Find the lengths of its sides.
In parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF : FE = 5 : 3 and area of △ ADF is 60 cm2; find :
(i) area of △ ADE
(ii) if AE : EB = 4 : 5, find the area of △ ADB.
(iii) also, find area of parallelogram ABCD.
In the following figure, OAB is a triangle and AB // DC.
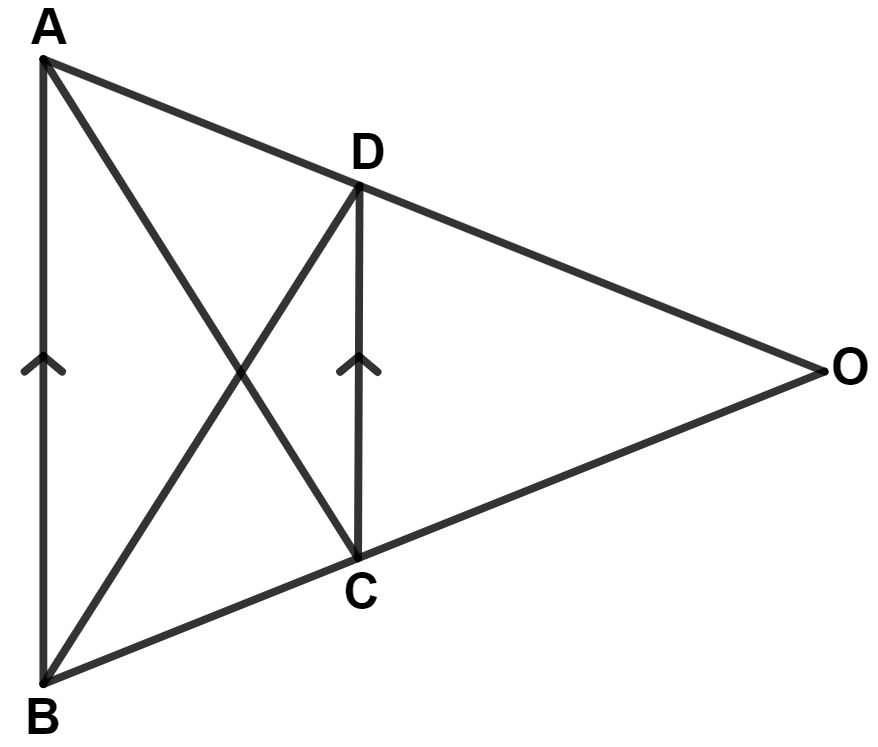
If the area of △ CAD = 140 cm2 and the area of △ ODC = 172 cm2, find
(i) the area of △ DBC
(ii) the area of △ OAC
(iii) the area of △ ODB
E, F, G and H are the mid-points of the sides of a parallelogram ABCD. Show that area of quadrilateral EFGH is half of the area of parallelogram ABCD.