Mathematics
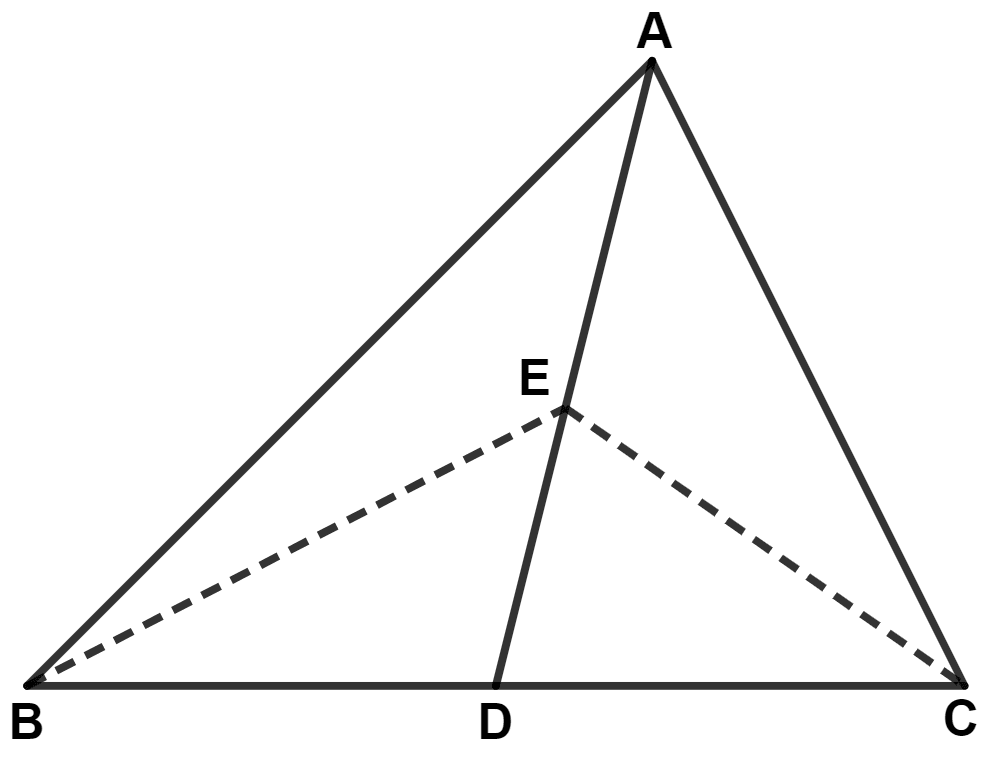
In the following figure, DE is parallel to BC. Show that :
(i) Area (△ ADC) = Area (△ AEB)
(ii) Area (△ BOD) = Area (△ COE)
Theorems on Area
24 Likes
Answer
We know that,
Triangles on the same base and between the same parallel lines are equal in area.
Since, triangle DEB and DEC lie on the same base DE and between the same parallel lines DE and BC.
∴ Area of △ DEC = Area of △ DEB ………(1)
(i) Adding area of △ ADE in both sides of the equation (1), we get :
⇒ Area of △ DEC + Area of △ ADE = Area of △ DEB + Area of △ ADE
⇒ Area of △ ADC = Area of △ AEB.
Hence, proved that area of △ ADC = area of △ AEB.
(ii) Subtracting area of △ DOE in both sides of the equation (1), we get :
⇒ Area of △ DEC - Area of △ DOE = Area of △ DEB - Area of △ DOE
⇒ Area of △ COE = Area of △ BOD.
Hence, proved that area of △ BOD = area of △ COE.
Answered By
13 Likes
Related Questions
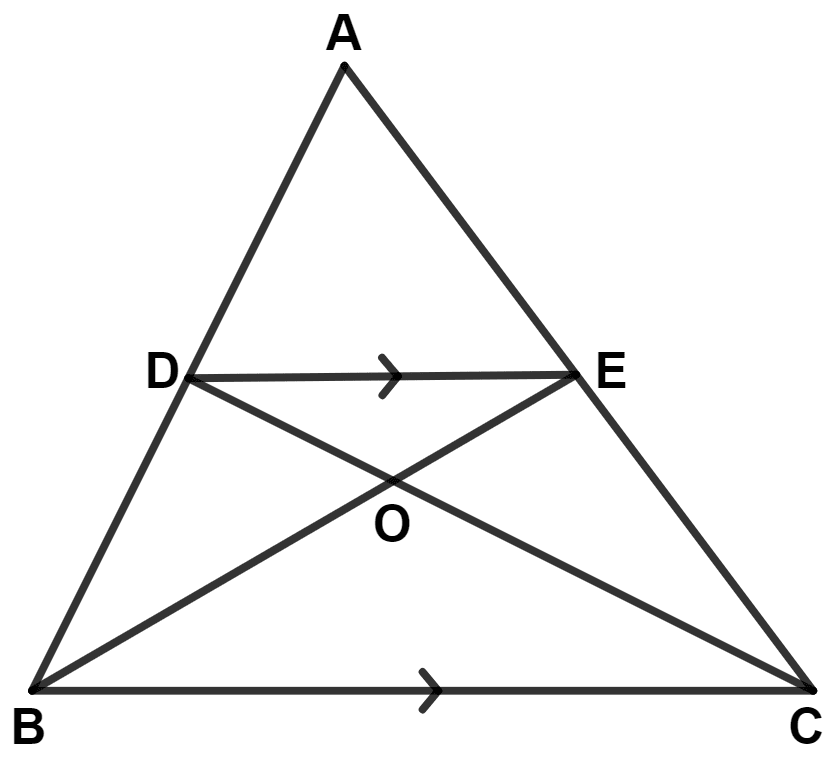
In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
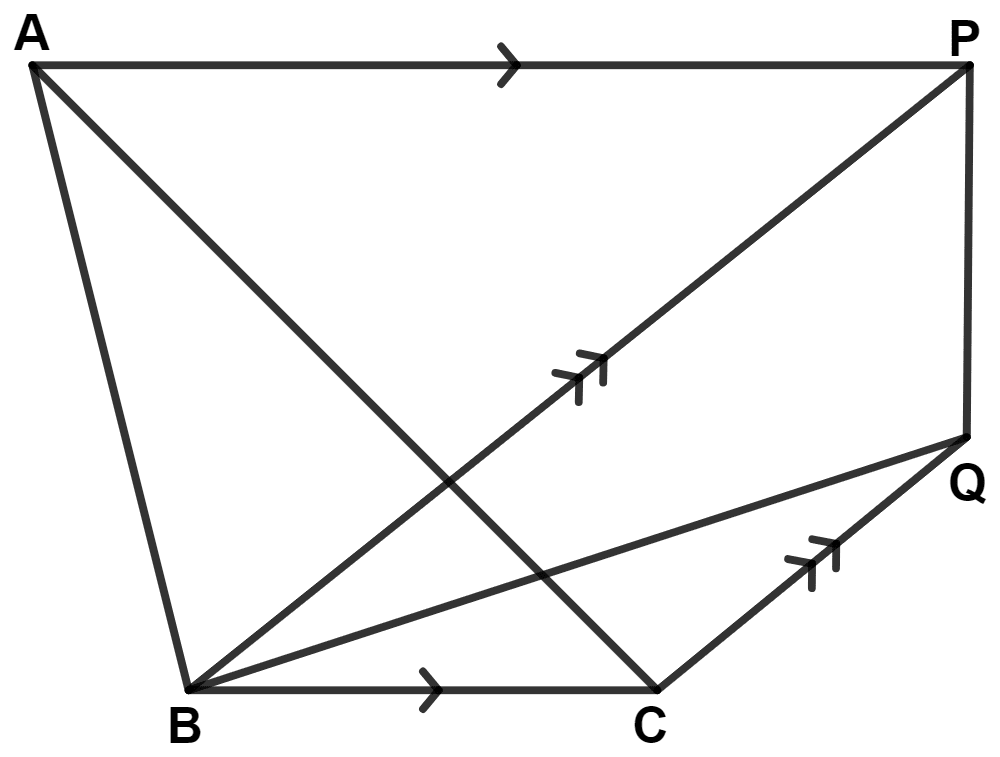
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH is perpendicular to FG, prove that :
(i) △ EAC ≅ △ BAF
(ii) Area of the square ABDE = Area of the rectangle ARHF.
Show that :
(i) a diagonal divides a parallelogram into two triangles of equal area.
(ii) the ratio of the areas of two triangles of the same height is equal to the ratio of their bases.
(iii) the ratio of the areas of two triangles on the same base is equal to the ratio of their heights.
In the given figure; AD is median of △ ABC and E is any point on median AD. Prove that Area (△ ABE) = Area (△ ACE).