Mathematics
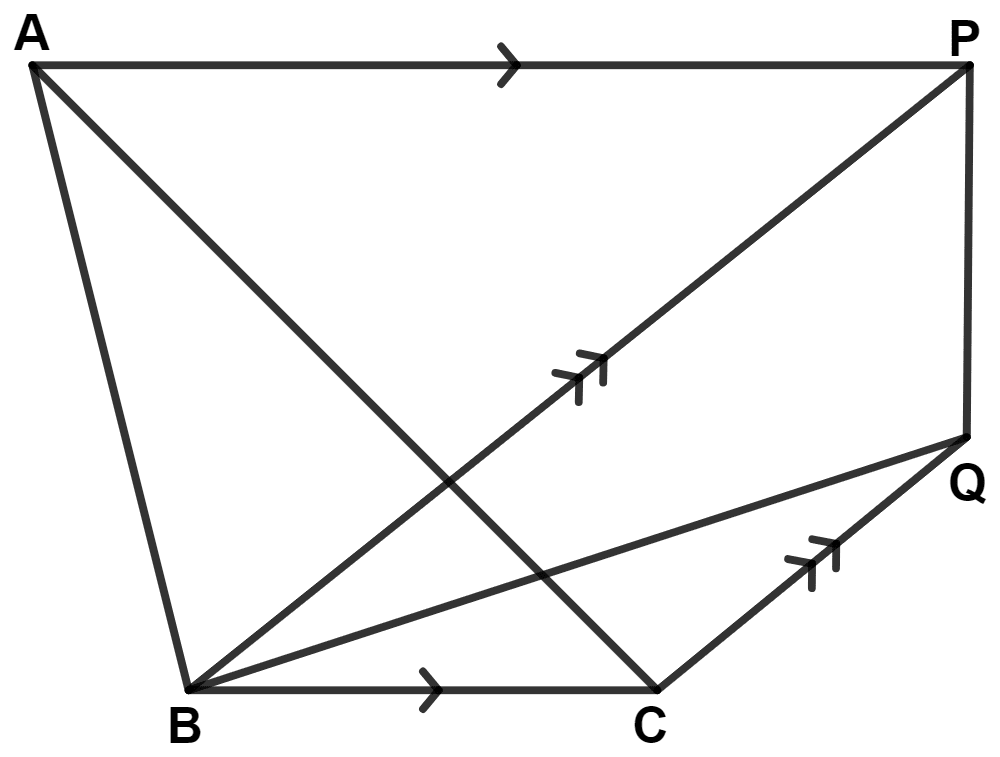
In the given figure, AP is parallel to BC, BP is parallel to CQ. Prove that the areas of triangles ABC and BQP are equal.
Theorems on Area
23 Likes
Answer
We know that,
Triangles on the same base and between the same parallel lines are equal in area.
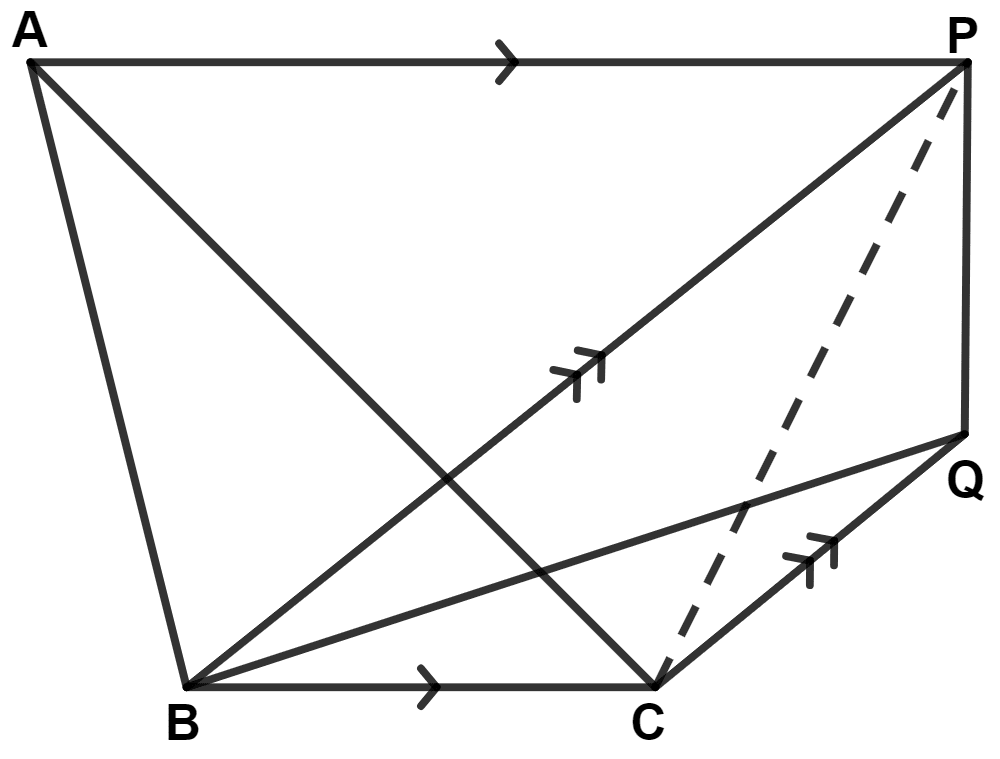
Since, triangle ABC and BPC lie on the same base BC and between the same parallel lines AP and BC.
∴ Area of △ ABC = Area of △ BPC ………(1)
Since, triangle BPC and BQP lie on the same base BP and between the same parallel lines BP and CQ.
∴ Area of △ BPC = Area of △ BQP ………(2)
From equations (1) and (2), we get :
Area of △ ABC = Area of △ BQP.
Hence, proved that area of △ ABC = area of △ BQP.
Answered By
13 Likes
Related Questions
ABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q. Prove that triangle BCP is equal in area to triangle DPQ.
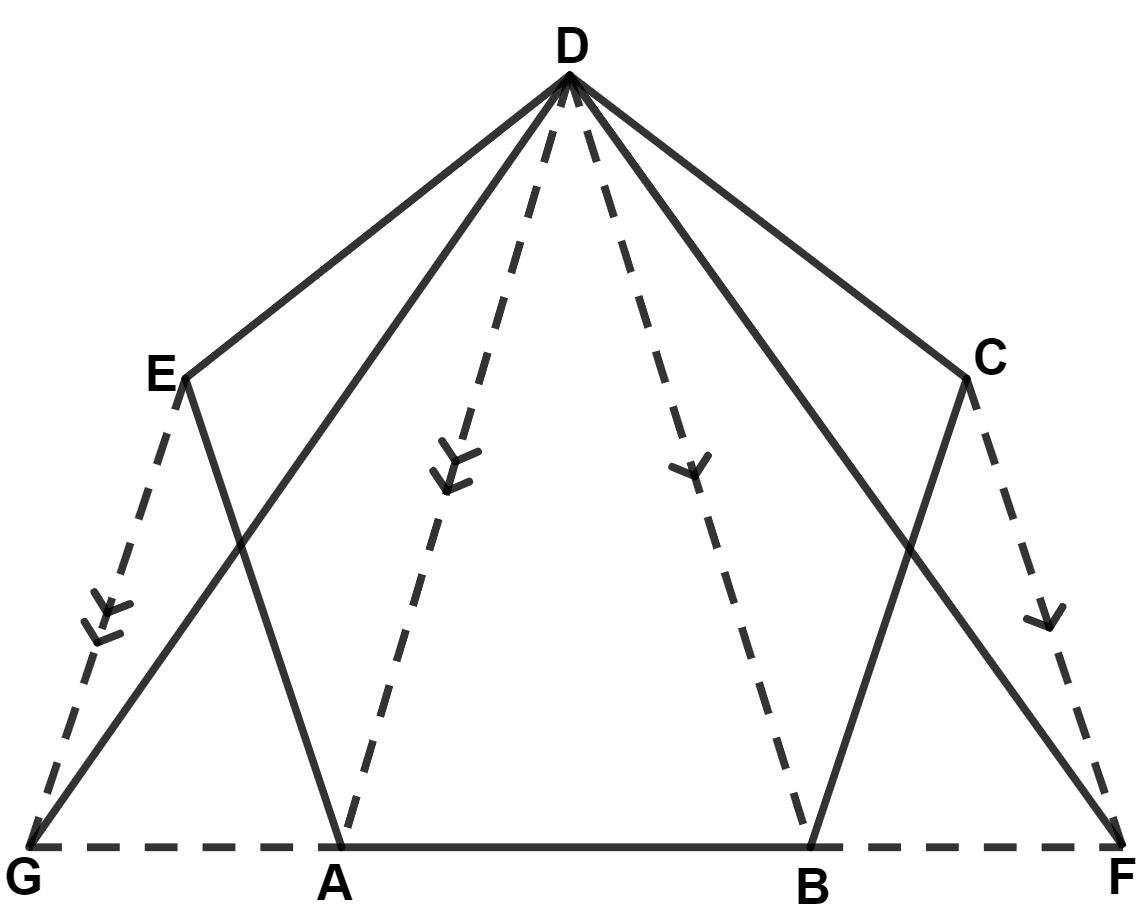
The given figure shows a pentagon ABCDE. EG drawn parallel to DA meets BA produced at G and CF drawn parallel to DB meets AB produced at F. Prove that the area of pentagon ABCDE is equal to the area of triangle GDF.
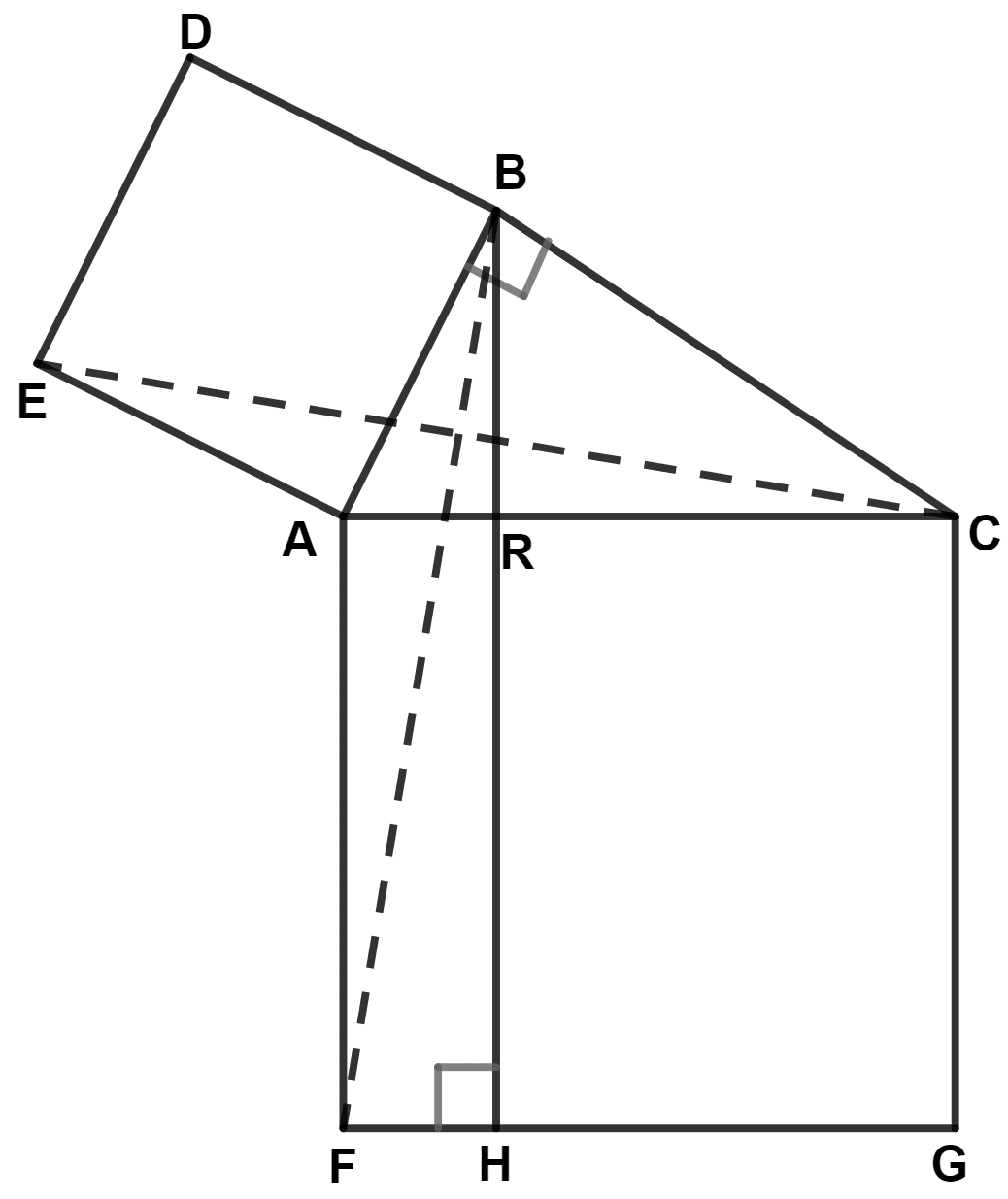
In the figure given alongside, squares ABDE and AFGC are drawn on the side AB and the hypotenuse AC of the right triangle ABC.
If BH is perpendicular to FG, prove that :
(i) △ EAC ≅ △ BAF
(ii) Area of the square ABDE = Area of the rectangle ARHF.
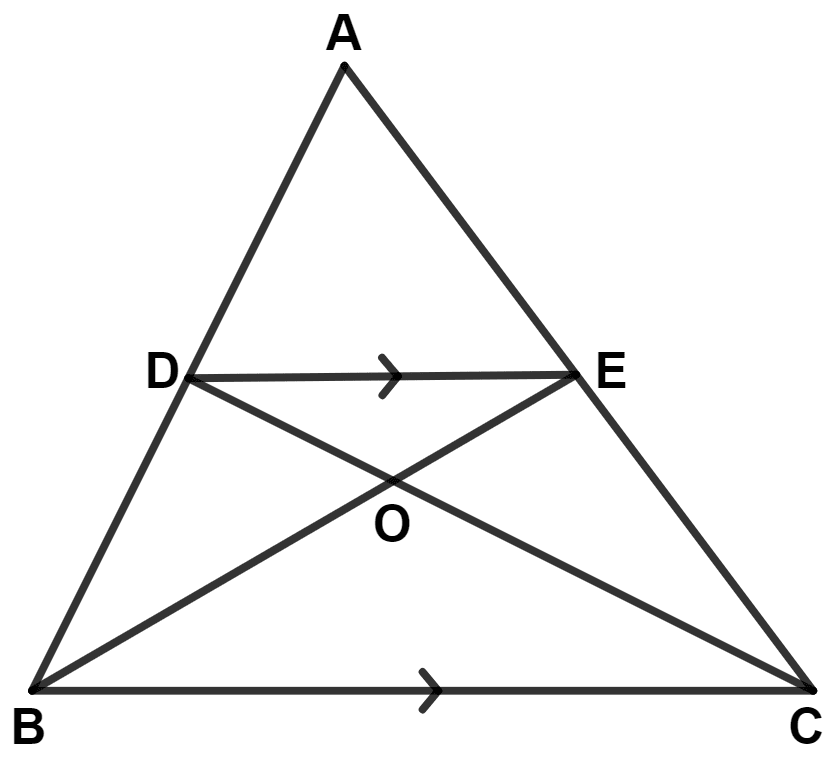
In the following figure, DE is parallel to BC. Show that :
(i) Area (△ ADC) = Area (△ AEB)
(ii) Area (△ BOD) = Area (△ COE)