Mathematics
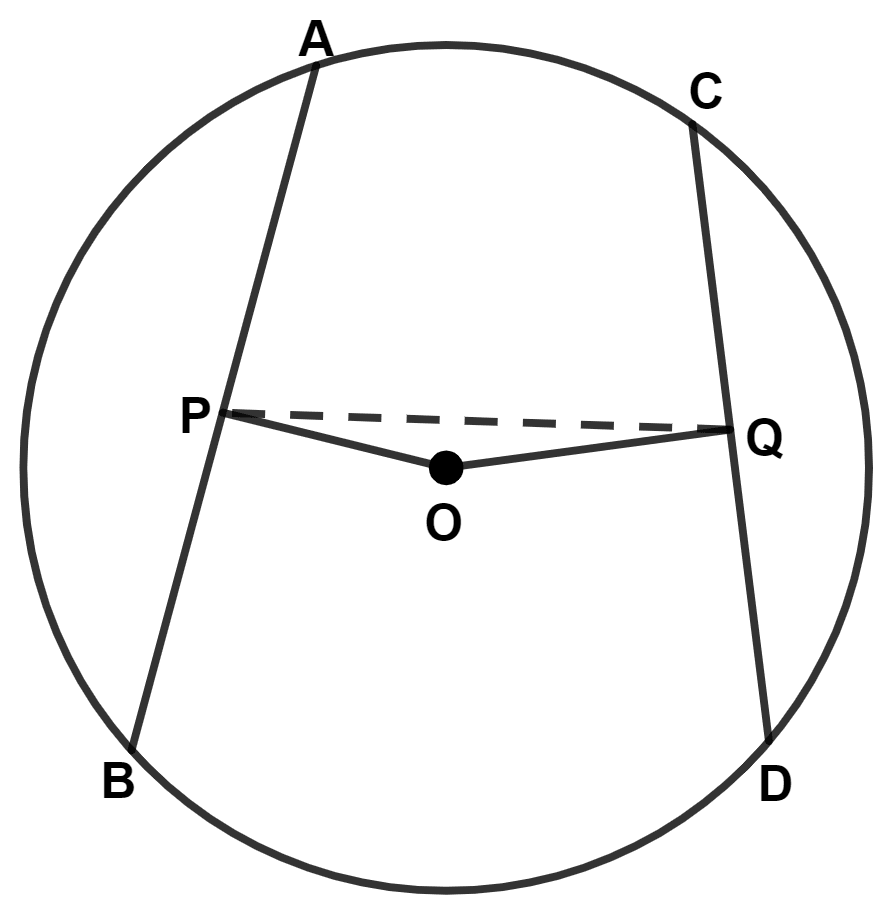
In the given figure, AB and CD are two equal chords of a circle, with center O.
If P is the mid-point of chord AB. Q is the mid-point of chord CD and ∠POQ = 150°, find ∠APQ.
Circles
8 Likes
Answer
We know that,
Equal chords are equidistant from the center.
∴ OP = OQ
In △ OPQ,
⇒ OP = OQ
⇒ ∠OQP = ∠OPQ = x (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠OQP + ∠OPQ + ∠POQ = 180°
⇒ x + x + 150° = 180°
⇒ 2x = 180° - 150°
⇒ 2x = 30°
⇒ x = = 15°.
We know that,
A straight line drawn from the center of the circle to bisect the chord, which is not a diameter, is at right angles to the chord.
∴ ∠OPA = 90°
From figure,
⇒ ∠APQ = ∠OPA - ∠OPQ = 90° - x = 90° - 15° = 75°.
Hence, ∠APQ = 75°.
Answered By
6 Likes
Related Questions
In a circle of radius 10 cm, AB and CD are two parallel chords of lengths 16 cm and 12 cm respectively. Calculate the distance between the chords, if they are on :
(i) the same side of the center
(ii) the opposite side of the center
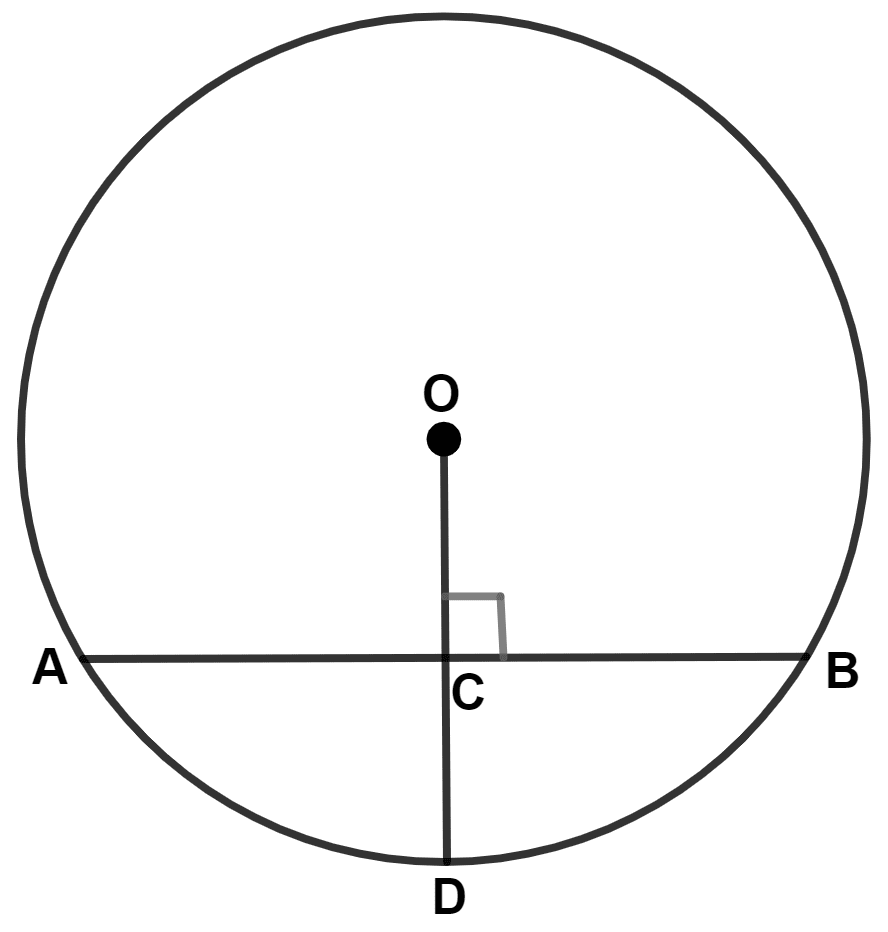
In the given figure, O is the center of the circle with radius 20 cm and OD is perpendicular to AB.
If AB = 32 cm, find the length of CD.
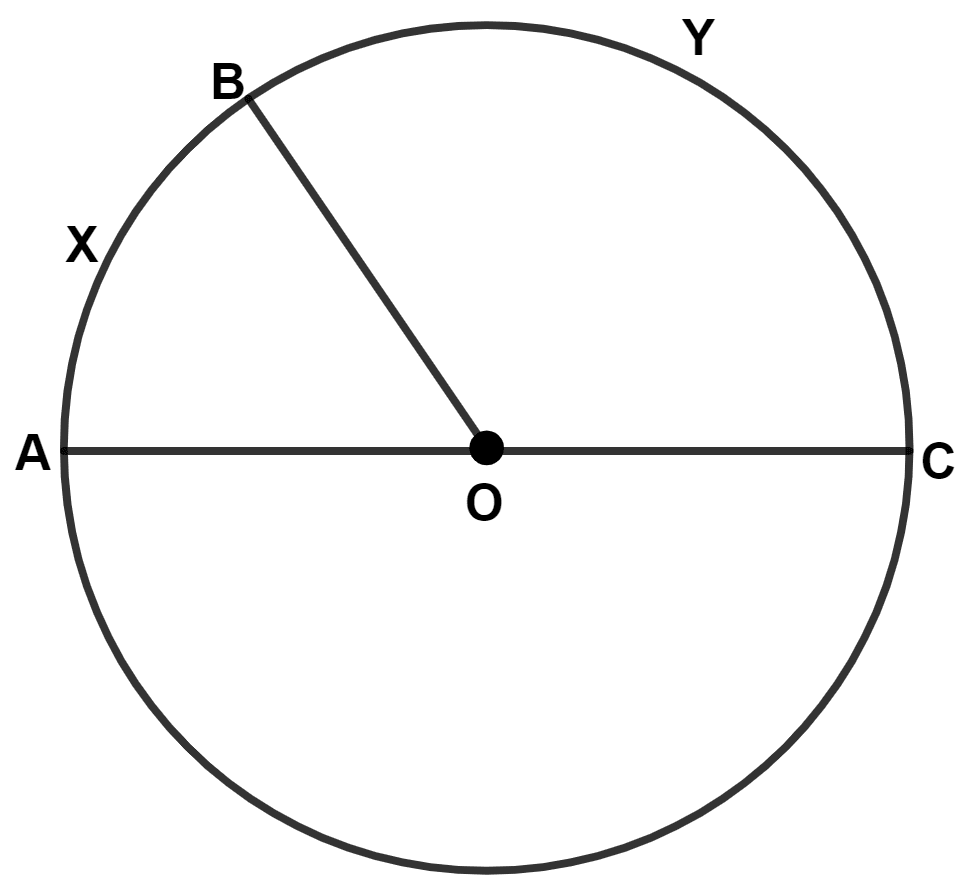
In the given figure, AOC is the diameter of the circle, with center O. If arc AXB is half of arc BYC, find ∠BOC.
The circumference of a circle, with center O, is divided into three arcs APB, BQC and CRA such that :
Find ∠BOC.