Mathematics
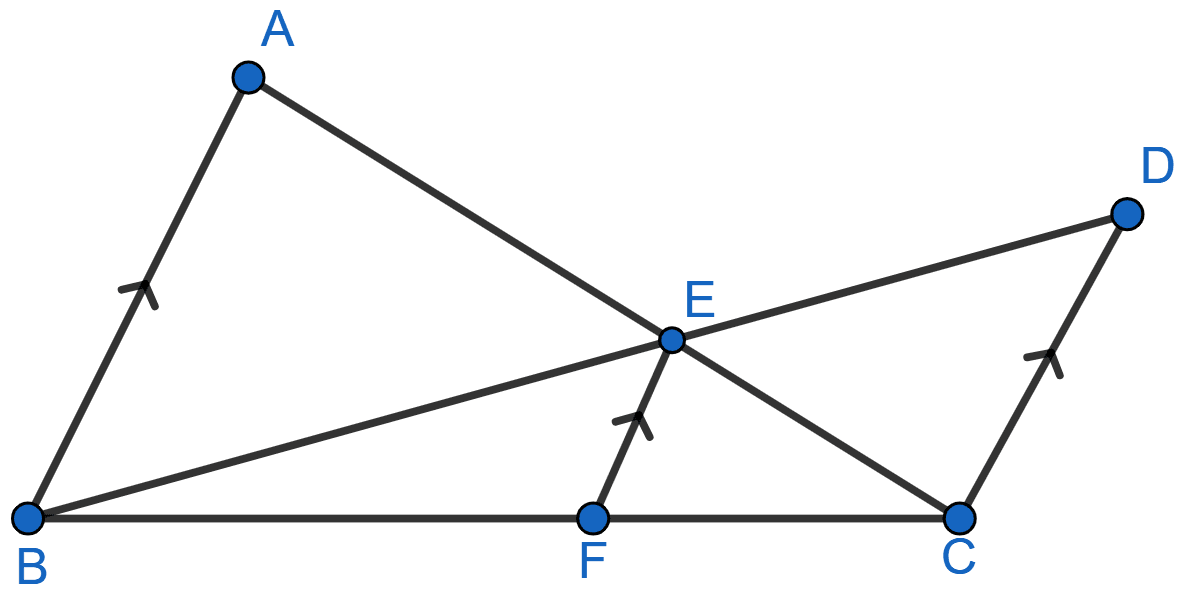
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the length of EC and EF.
Similarity
36 Likes
Answer
(i) The three pairs of similar triangle are :
In △BEF and △BDC
⇒ ∠FBE = ∠CBD [Common angle]
⇒ ∠BFE = ∠BCD [Corresponding angles are equal]
∴ △BEF ~ △BDC [By AA]
In △CEF and △CAB
⇒ ∠FCE = ∠BCA [Common angle]
⇒ ∠CFE = ∠CBA [Corresponding angles are equal]
∴ △CEF ~ △CAB [By AA]
In △ABE and △CDE
⇒ ∠AEB = ∠CED [Vertically opposite angles are equal]
⇒ ∠BAE = ∠ECD [Alternate angles are equal]
∴ △ABE ~ △CDE [By AA]
(ii) Since, △ABE and △CDE are similar,
Since, △CEF and △CAB are similar,
Hence, CE = 31.5 cm and EF = cm.
Answered By
20 Likes
Related Questions
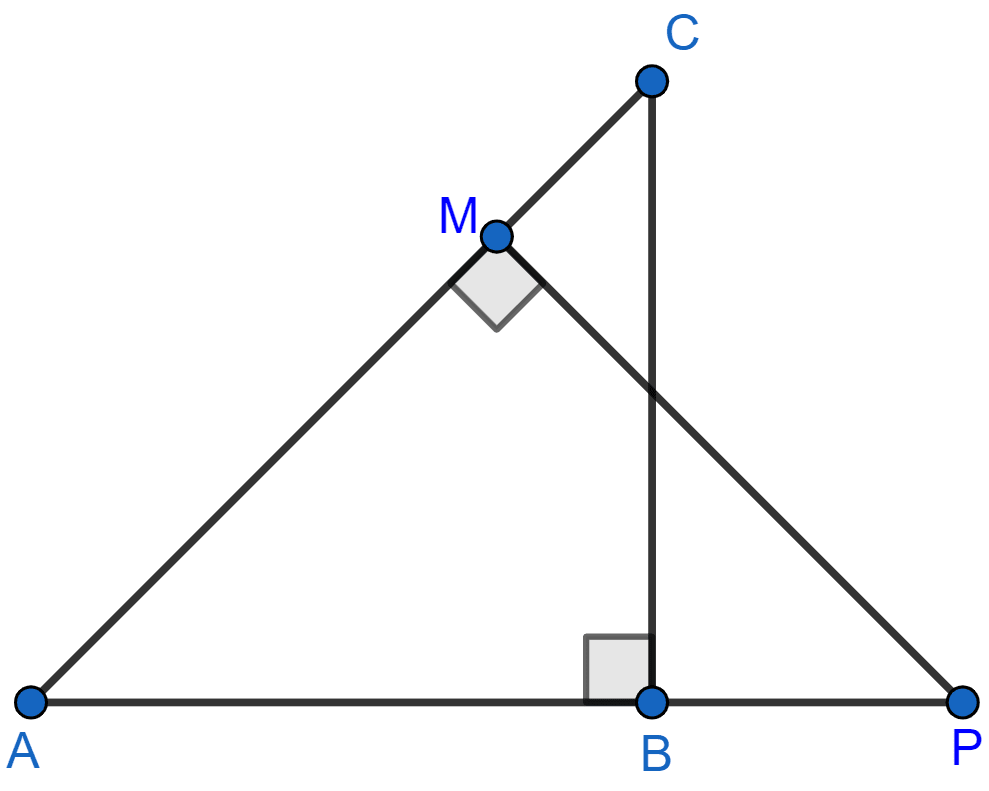
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove that : ∆ABC ~ ∆AMP.
(ii) Find AB and BC.
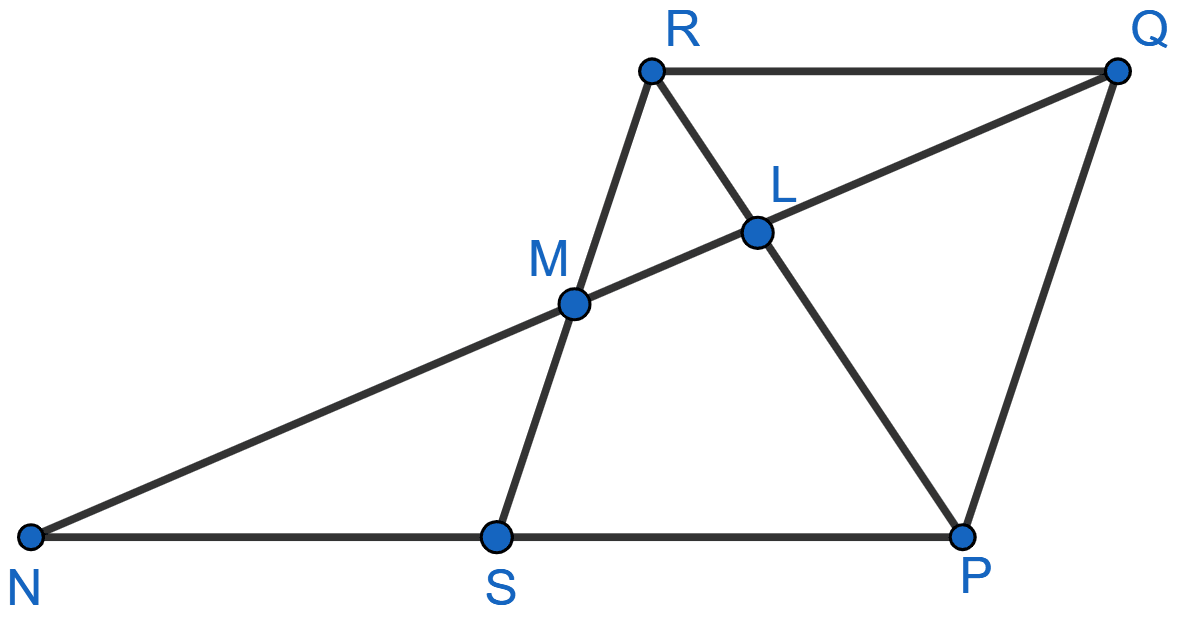
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm, L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N. Find the lengths of PN and RM.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
(i) Calculate the ratio PQ : AC, giving reason for your answer.
(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.

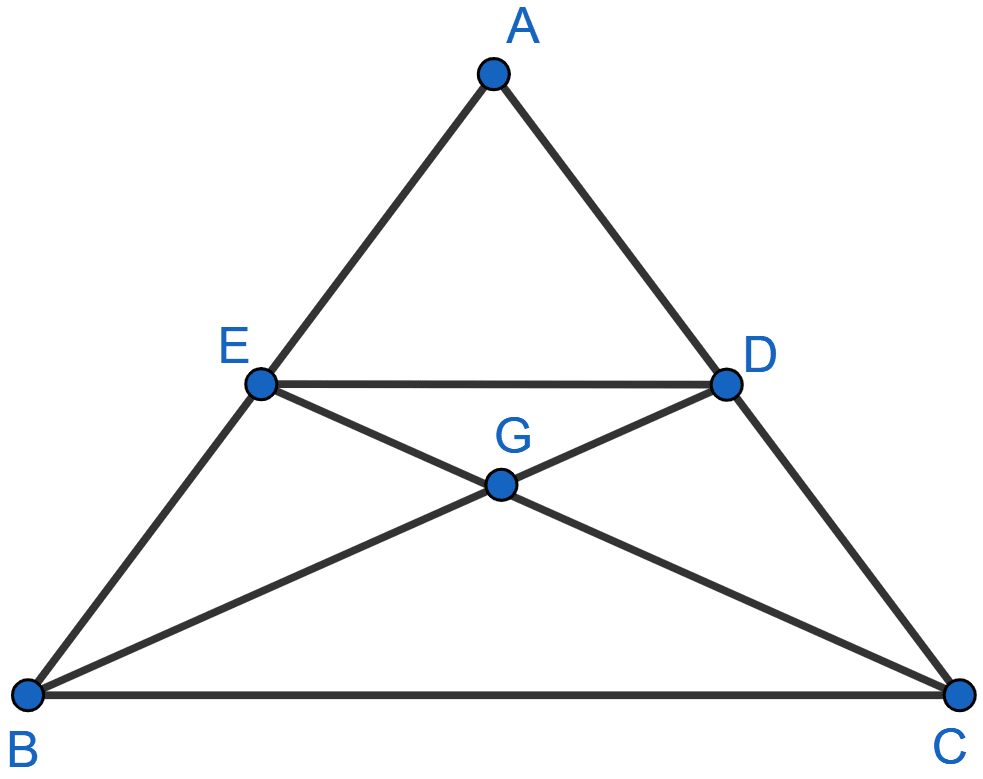
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that :
(i) △EGD ~ △CGB and
(ii) BG = 2GD from (i) above.