Mathematics
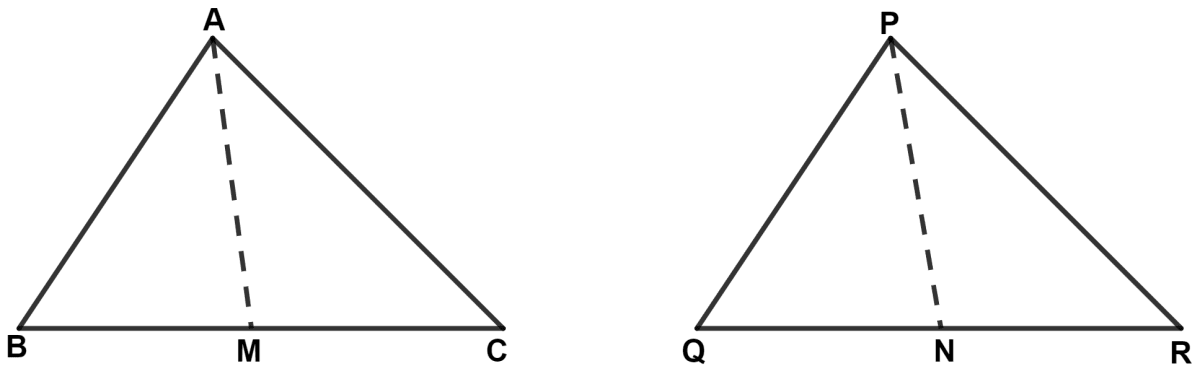
In the given figure, AB = PQ, BC = QR and median AM = median PN, then :
AC ≠ PR
BM ≠ QN
△ ABM ≅ △ PQN
△ ABC ≅ △ PQR
Triangles
25 Likes
Answer
Given,
AM and PN are medians of triangle ABC and PQR.
∴ BM = MC and QN = NR.
BC = QR (Given)
⇒
⇒ BM = QN.
In △ ABM and △ PQN,
⇒ AB = PQ (Given)
⇒ AM = PN (Given)
⇒ BM = QN (Proved above)
∴ △ ABM ≅ △ PQN (By S.S.S. axiom)
We know that,
Corresponding parts of congruent triangles are equal.
∴ ∠AMB = ∠PNQ (By C.P.C.T.C.)
⇒ 180° - ∠AMB = 180° - ∠PNQ
⇒ ∠AMC = ∠PNR
Given,
⇒ BC = QR
⇒
⇒ MC = NR.
In △ AMC and △ PNR,
⇒ AM = PN (Given)
⇒ ∠AMC = ∠PNR (Proved above)
⇒ MC = NR (Proved above)
∴ △ AMC ≅ △ PNR (By S.A.S. axiom)
∴ AC = PR (By C.P.C.T.C.)
In △ ABC and △ PQR,
⇒ AB = PQ (Given)
⇒ BC = QR (Given)
⇒ AC = PR (Proved above)
∴ △ ABC ≅ △ PQR (By S.S.S. axiom)
Hence, Option 4 is the correct option.
Answered By
12 Likes
Related Questions
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced upto point R so that CR = BP.
Prove that QR bisects PC.

PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.
In triangles ABC and DEF, AB = DE and AC = EF, then to make these two triangles congruent, we must have :
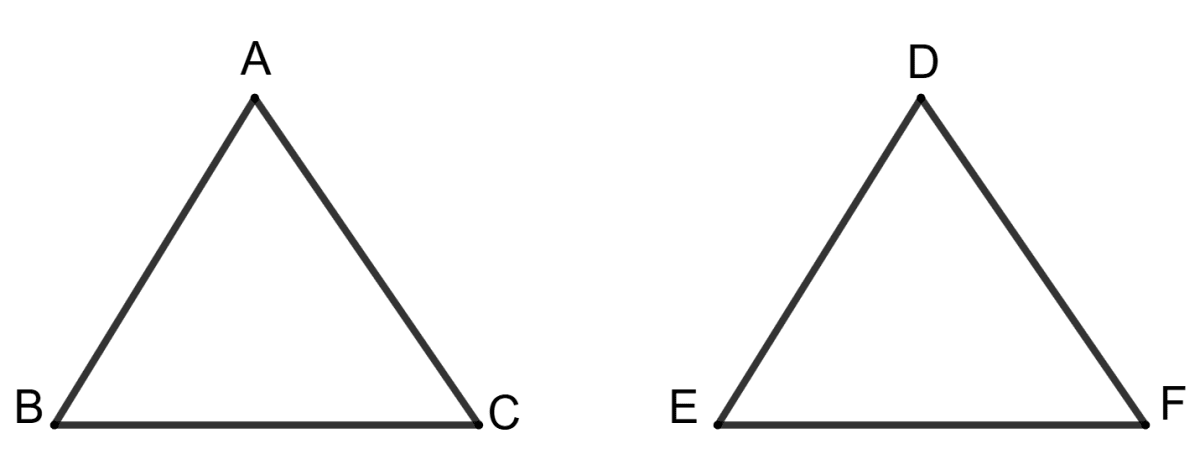
BC = DF
∠A = ∠E
any of (1) and (2)
none of (1) and (2)
In quadrilateral ABCD, AB = AC and BD = CD, then AD bisects :
angle ADC
angle BAD
angle BAC
angle ABC