Mathematics
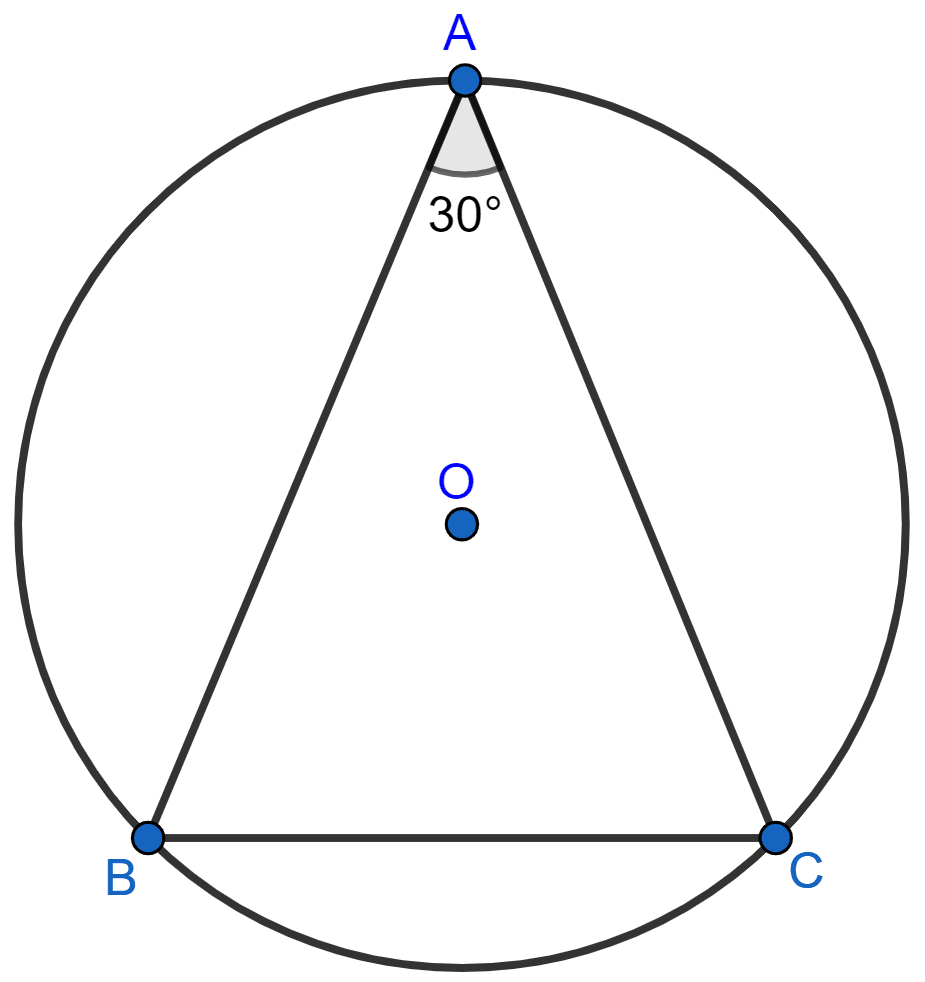
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.
Circles
32 Likes
Answer
Join OB and OC.
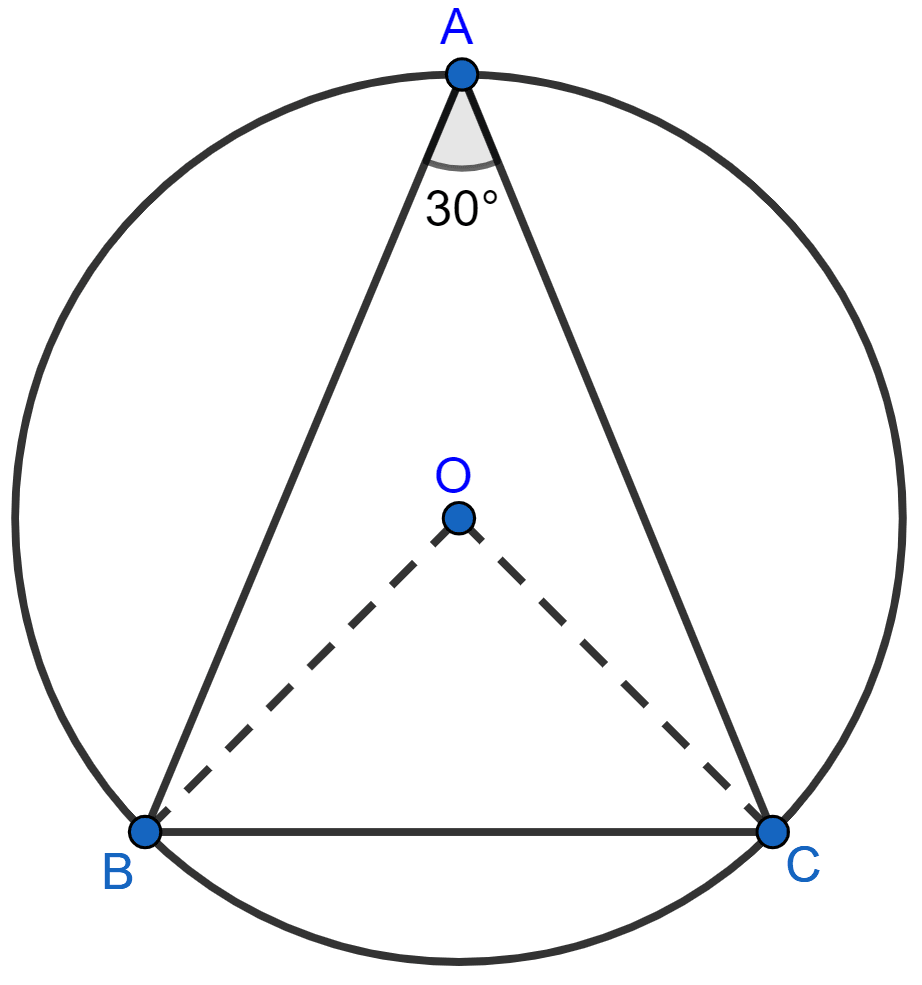
We know that,
Angle at the centre is twice the angle at remaining circumference.
∴ ∠BOC = 2∠BAC = 2 × 30° = 60°
In △OBC,
⇒ OB = OC [Radii of same circle]
⇒ ∠OBC = ∠OCB = x (let) [As angles opposite to equal sides are equal]
⇒ ∠BOC + ∠OBC + ∠OCB = 180°
⇒ 60° + x + x = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = = 60°.
∴ ∠OBC = ∠OCB = ∠BOC = 60°.
Hence, △OBC is an equilateral triangle.
∴ OB = OC = BC.
Hence, proved that BC is equal to the radius of the circumcircle of the triangle ABC.
Answered By
23 Likes
Related Questions
O is the center of the circle and ∠AOC = 120°.
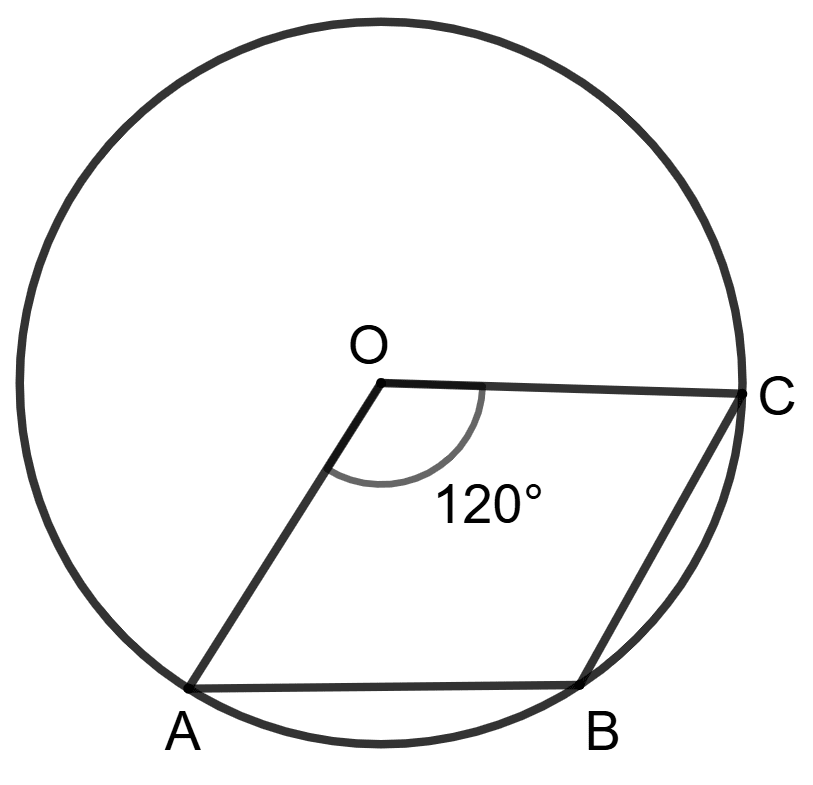
Statement (1) : ∠ABC = 120°
Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.
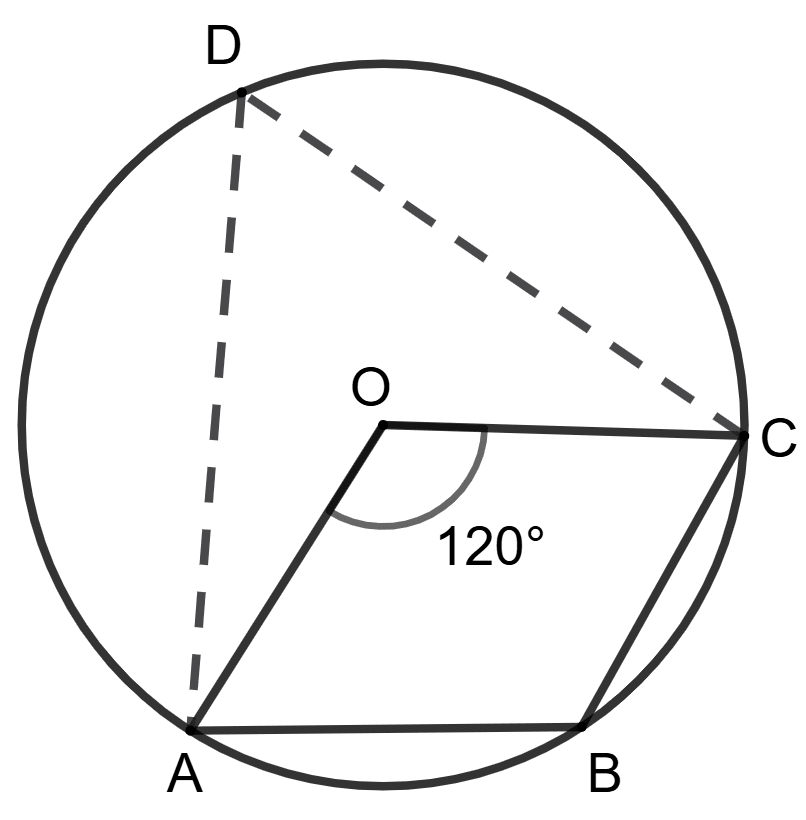
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
In the given circle with diameter AB, find the value of x.

Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.