Mathematics
O is the center of the circle and ∠AOC = 120°.
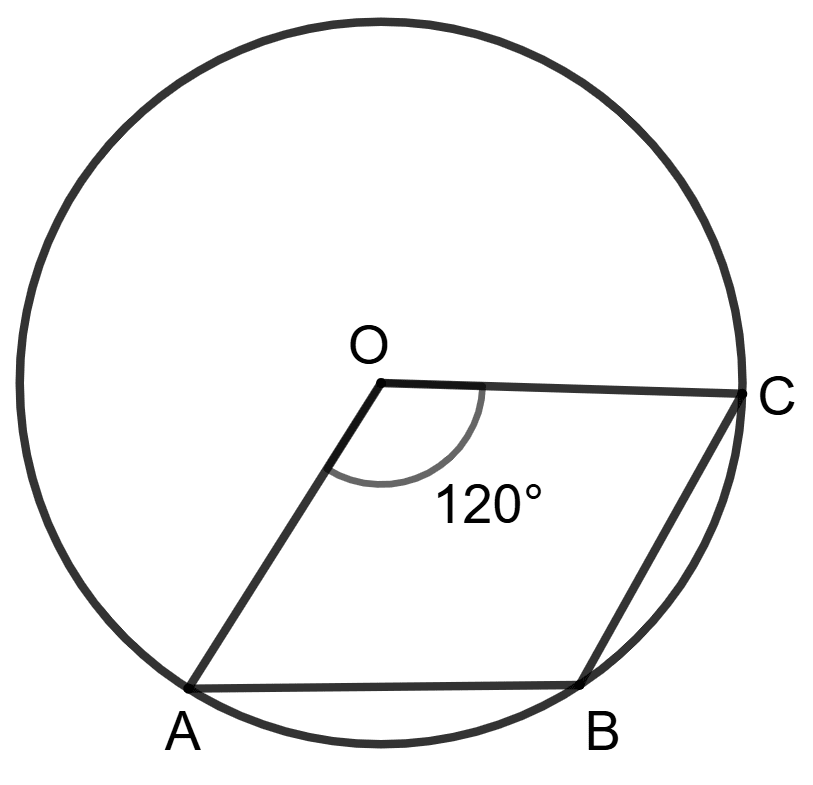
Statement (1) : ∠ABC = 120°
Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Circles
3 Likes
Answer
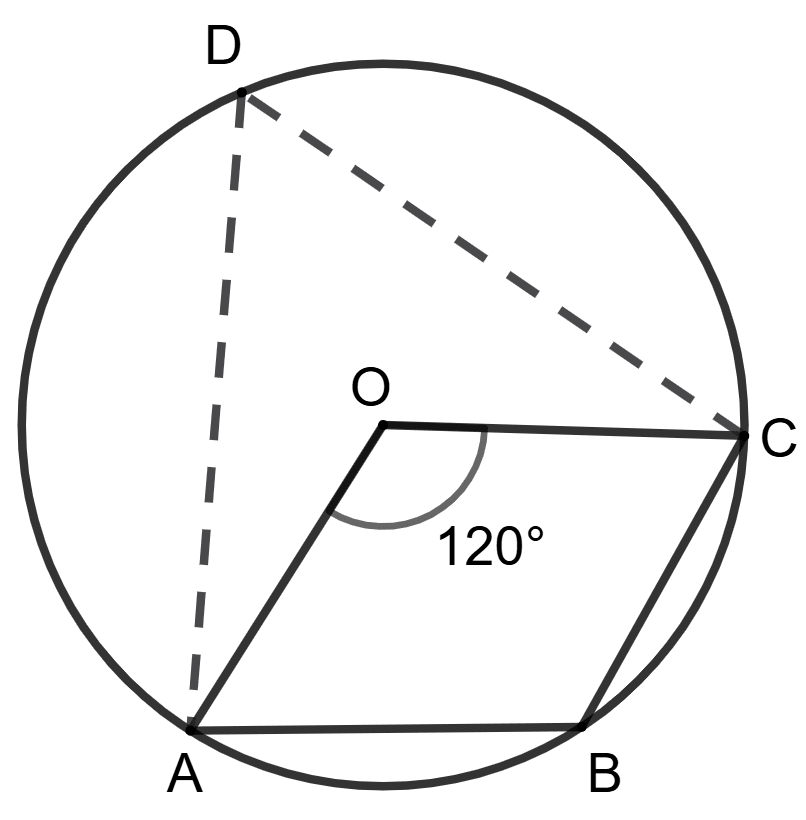
Since, the angle, which an arc of a circle subtends at the center of the circle is double the angle which it subtends at any point on the remaining part of the circumference.
⇒ ∠AOC = 2 x ∠ADC
⇒ 120° = 2 x ∠ADC
⇒ ∠ADC = = 60°
ABCD form a cyclic quadrilateral and sum of opposite angles of cyclic quadrilateral is 180°.
⇒ ∠ADC + ∠ABC = 180°
⇒ 60° + ∠ABC = 180°
⇒ ∠ABC = 180° - 60°
⇒ ∠ABC = 120°
So, both statement are true.
Hence, option 1 is the correct option.
Answered By
2 Likes
Related Questions
AC is diameter, AE is parallel to BC and ∠BAC = 50°.
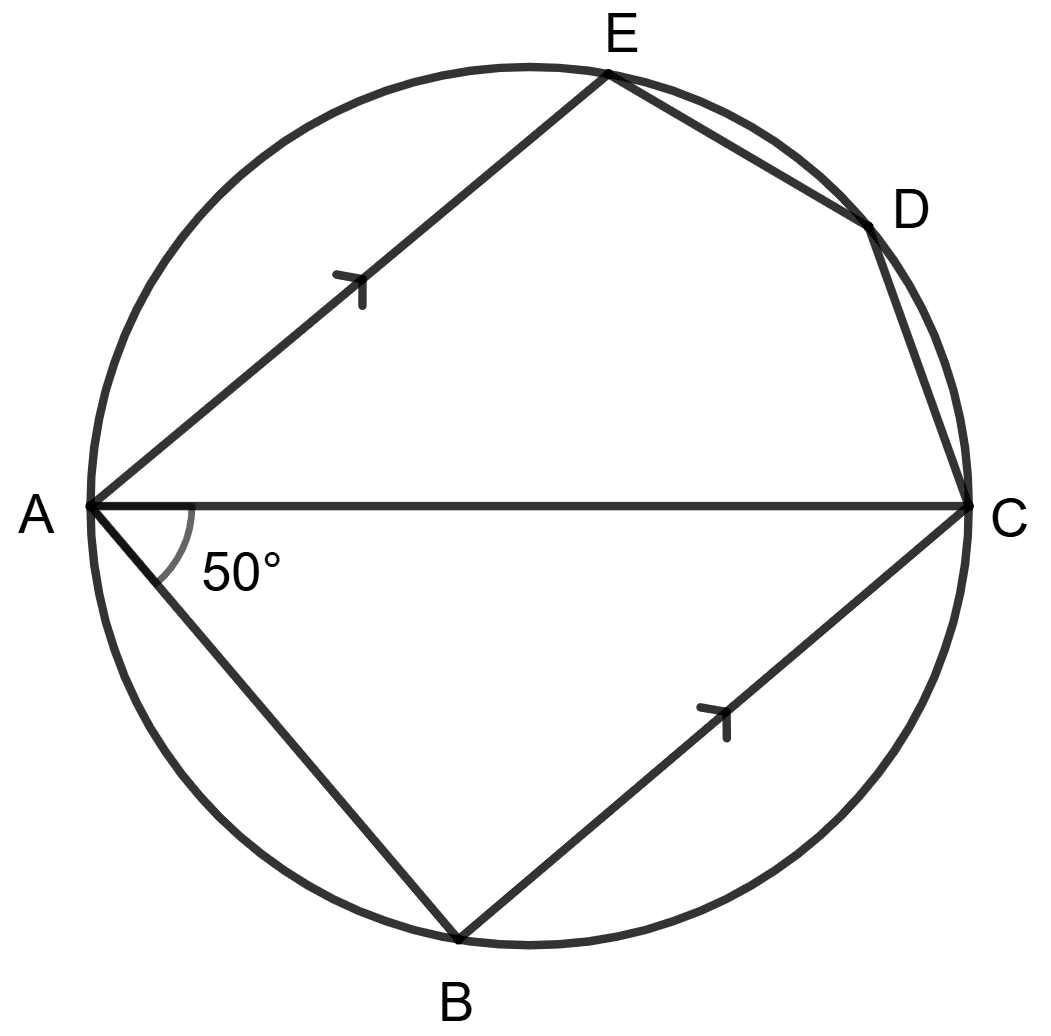
Statement (1) : ∠EDC + 50° = 180°.
Statement (2) : ∠EDC + ∠EAC = 180°.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is the center of the circle, OB = BC and ∠BOC = 20°.
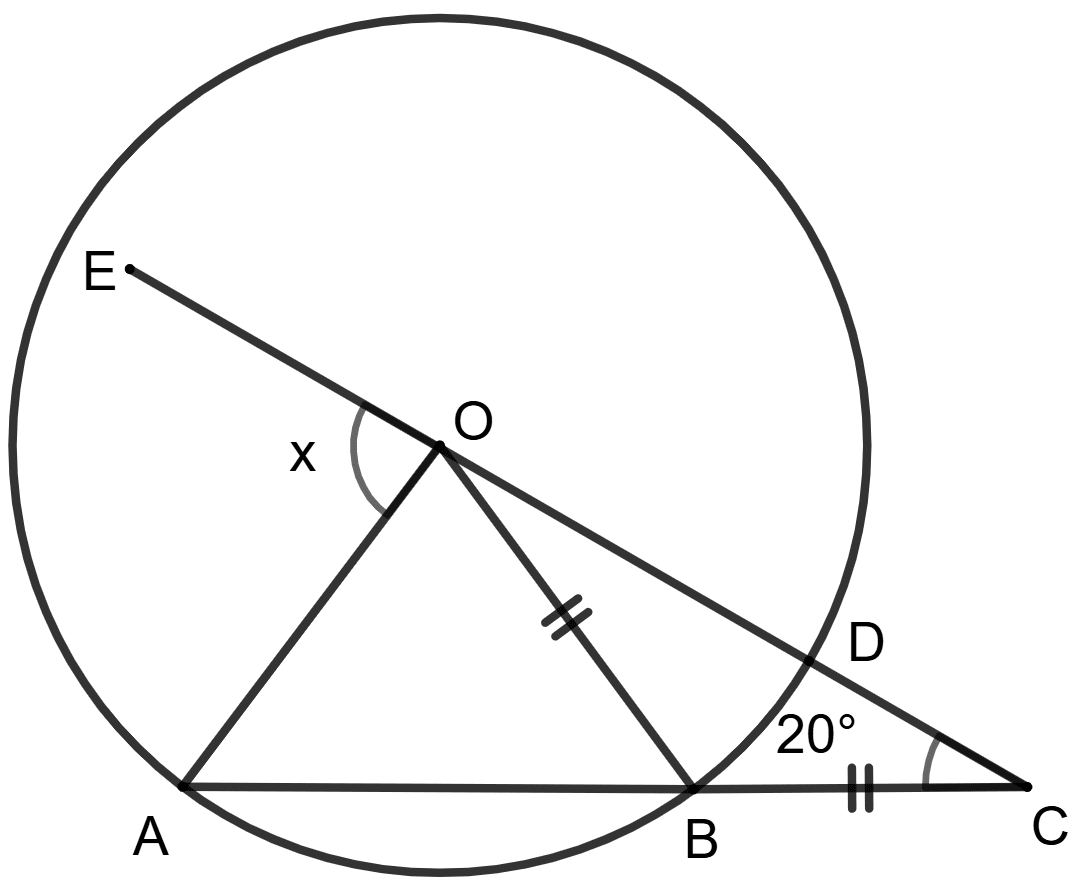
Statement (1) : x = 2 x 20° = 40°
Statement (2) : ∠BOC = 20°.
x = ∠OAB + 20° = ∠OBA + 20° = 40° + 20° = 60°
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
In the given circle with diameter AB, find the value of x.

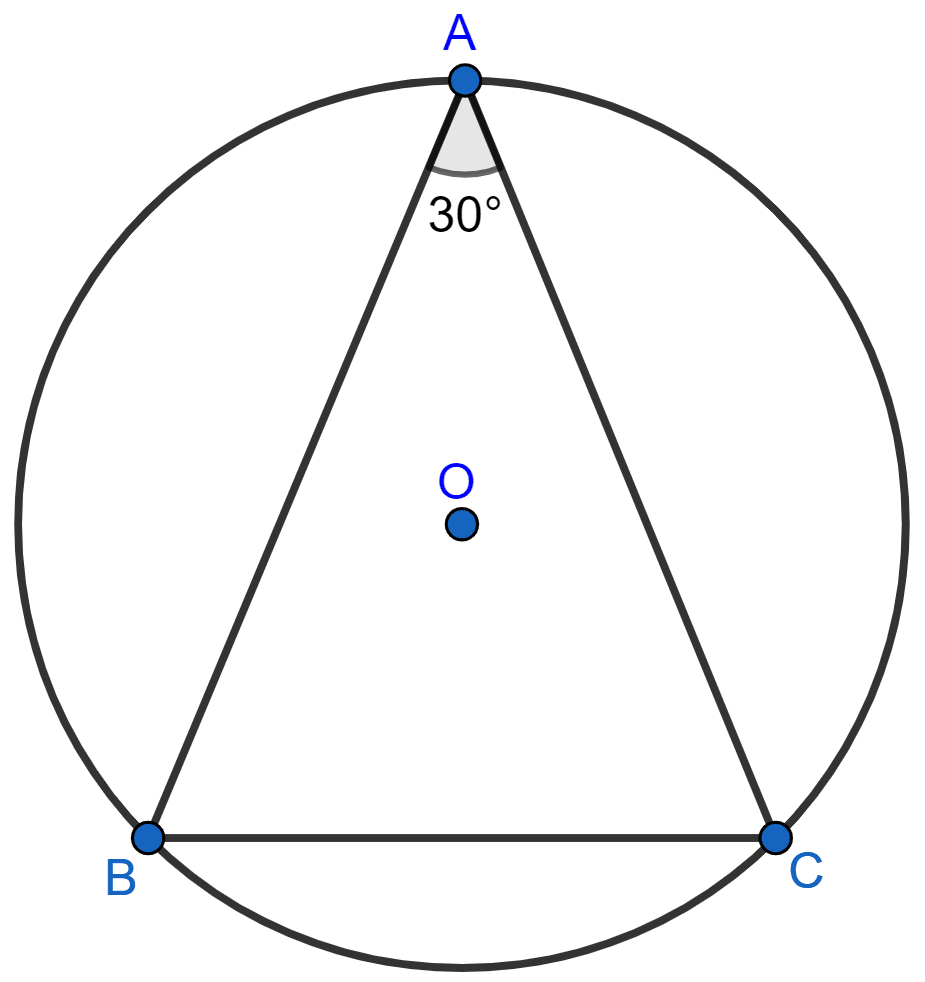
In the given figure, ABC is a triangle in which ∠BAC = 30°. Show that BC is equal to the radius of the circumcircle of the triangle ABC, whose centre is O.