Mathematics
AC is diameter, AE is parallel to BC and ∠BAC = 50°.
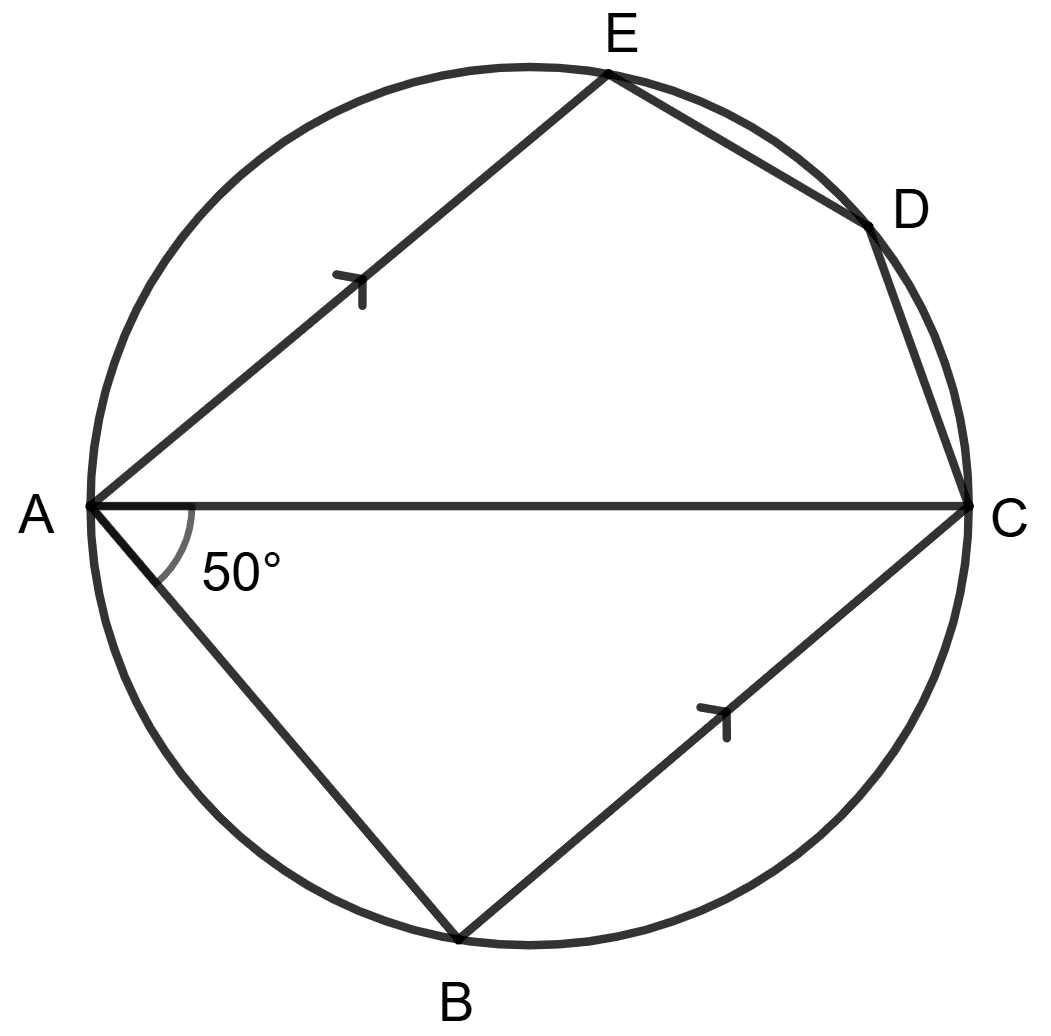
Statement (1) : ∠EDC + 50° = 180°.
Statement (2) : ∠EDC + ∠EAC = 180°.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Circles
1 Like
Answer
It is given that AC is diameter and angles in a semicircle is a right angle.
⇒ ∠ABC = 90°
Since, AE is parallel to BC and AB is transversal.
⇒ ∠ABC + ∠BAE = 180° [The sum of co-interior angles formed when a transversal intersects two parallel lines is always 180°]
⇒ 90° + ∠BAE = 180°
⇒ ∠BAE = 180° - 90°
⇒ ∠BAE = 90°
⇒ ∠BAC + ∠EAC = 90°
⇒ 50° + ∠EAC = 90°
⇒ ∠EAC = 90° - 50°
⇒ ∠EAC = 40°
AEDC form a cyclic quadrilateral and sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
⇒ ∠EDC + ∠EAC = 180°
⇒ ∠EDC + 40° = 180°
So, statement 1 is false but statement 2 is true.
Hence, option 4 is the correct option.
Answered By
3 Likes
Related Questions
Chords AC and BD intersect each other at point P.
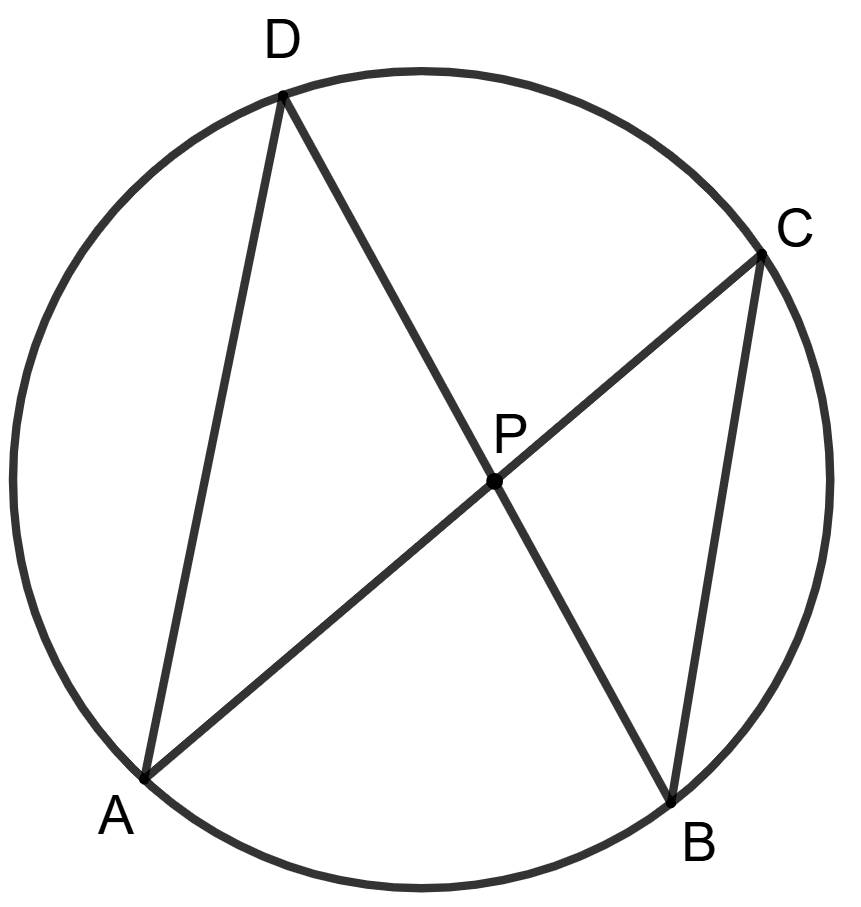
Assertion (A) : PA x PC = PB x PD.
Reason (R) : Δ APD ∼ Δ BPC
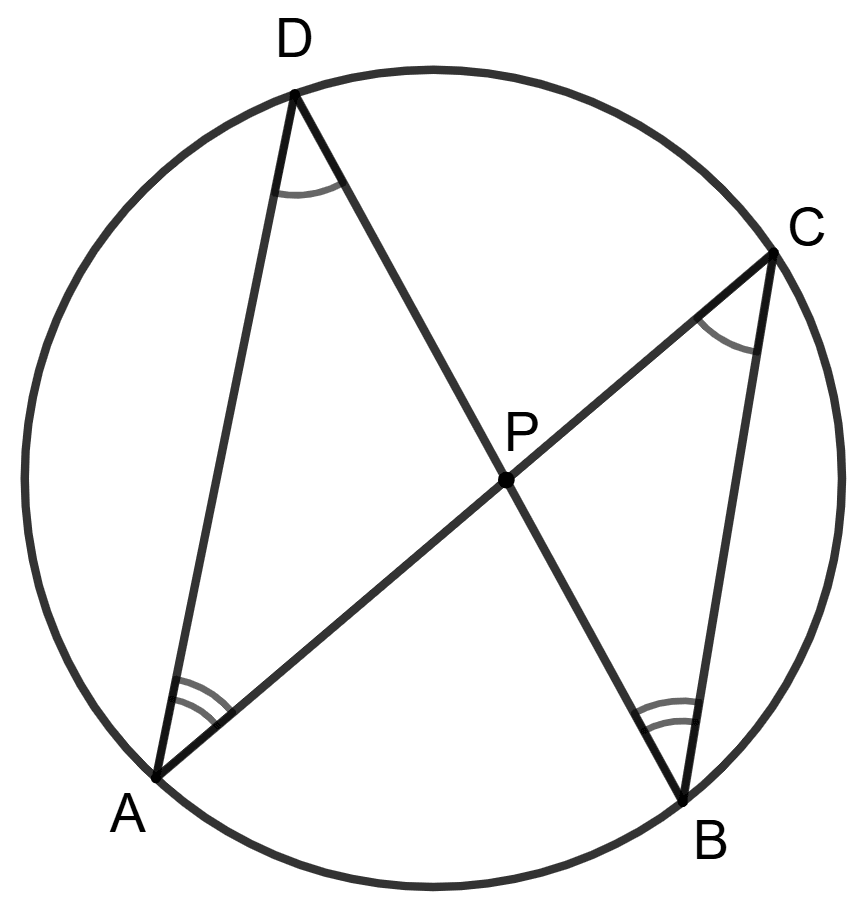
A is true, R is false.
A is false, R is true.
Both A and R are true and R is correct reason for A.
Both A and R are true and R is incorrect reason for A.
A circle with center at point O and ∠AOC = 160°.
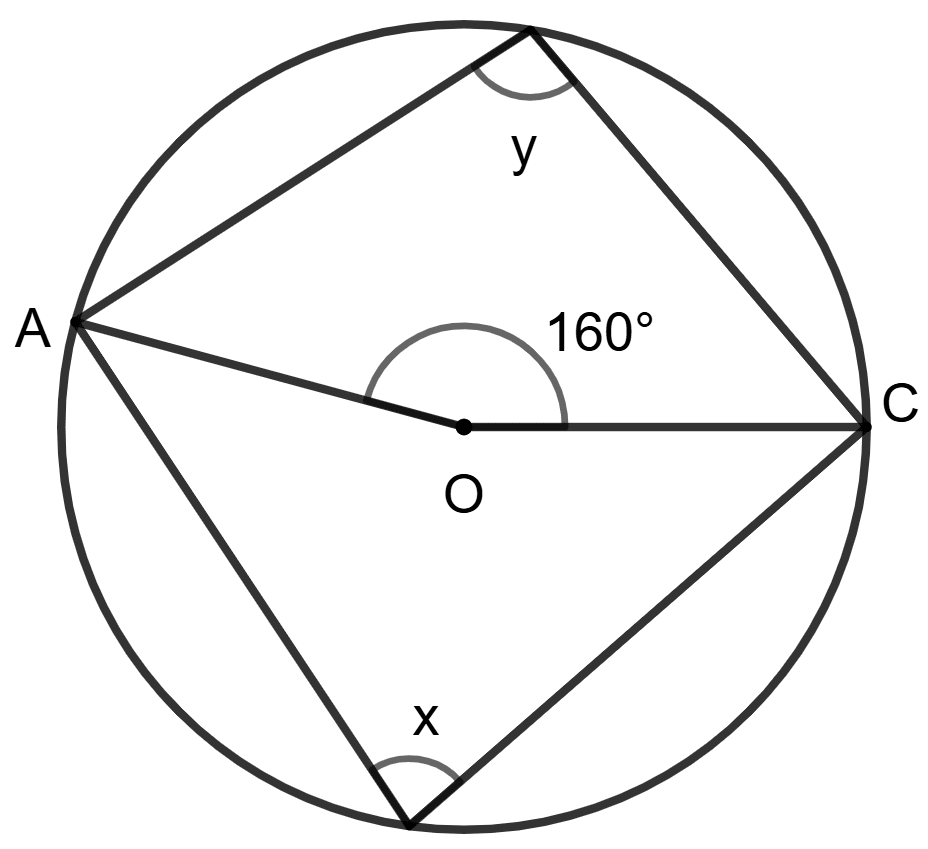
Statement (1) : Angle x = 100° and angle y = 80°.
Statement (2) : The angle, which an arc of a circle subtends at the center of the circle is double the angle which it subtends at any point on the remaining part of the circumference.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is the center of the circle, OB = BC and ∠BOC = 20°.
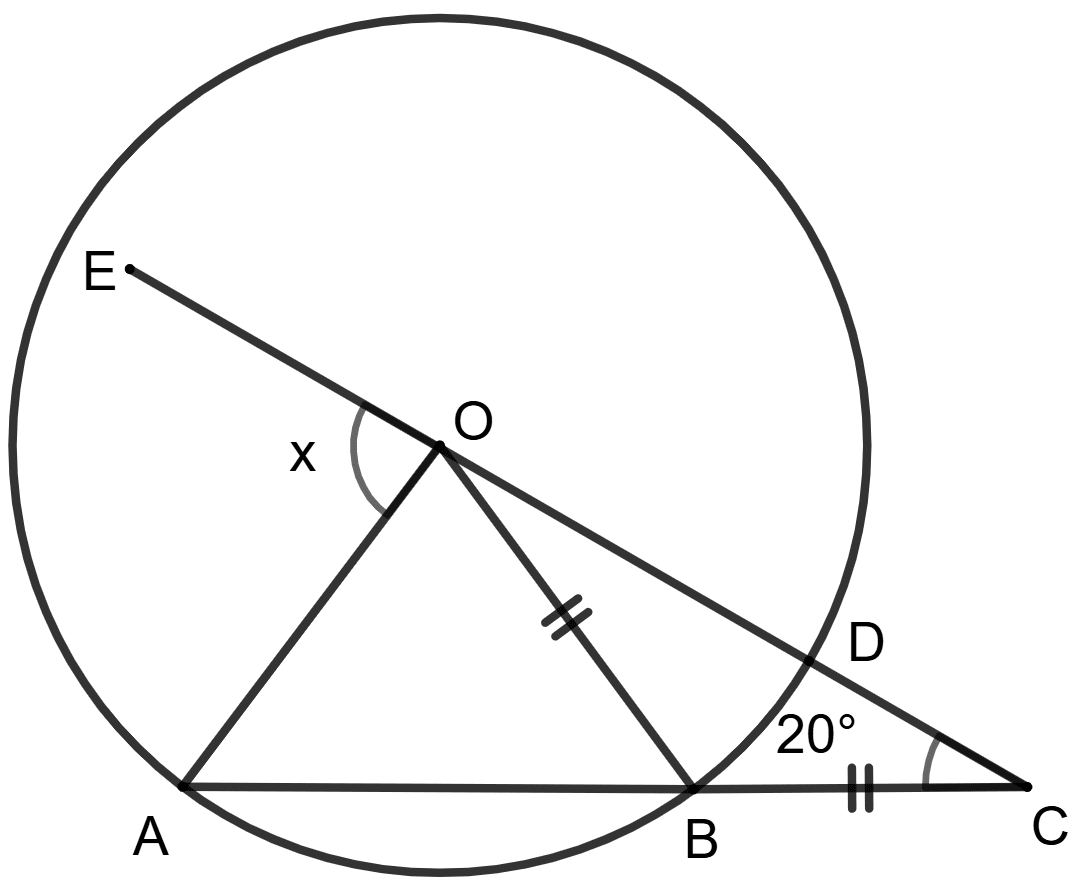
Statement (1) : x = 2 x 20° = 40°
Statement (2) : ∠BOC = 20°.
x = ∠OAB + 20° = ∠OBA + 20° = 40° + 20° = 60°
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is the center of the circle and ∠AOC = 120°.
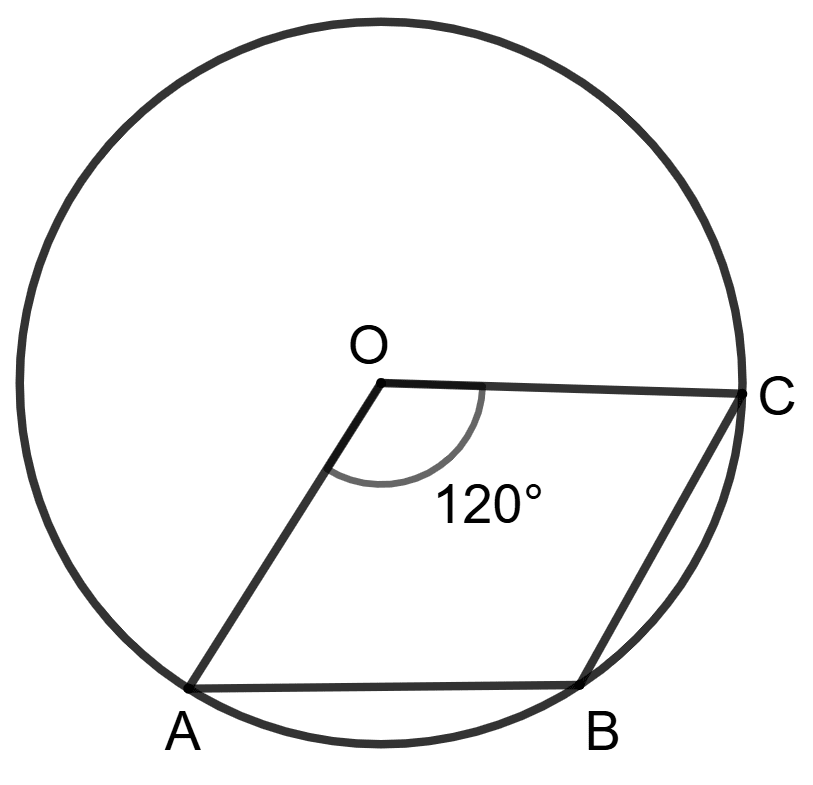
Statement (1) : ∠ABC = 120°
Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.
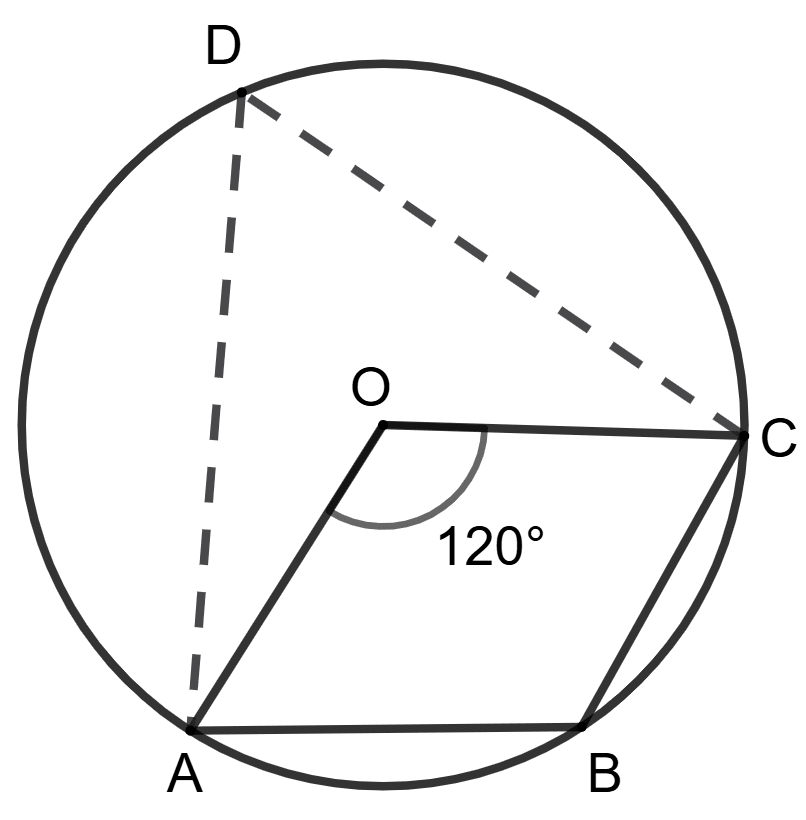
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.