Mathematics
O is the center of the circle, OB = BC and ∠BOC = 20°.
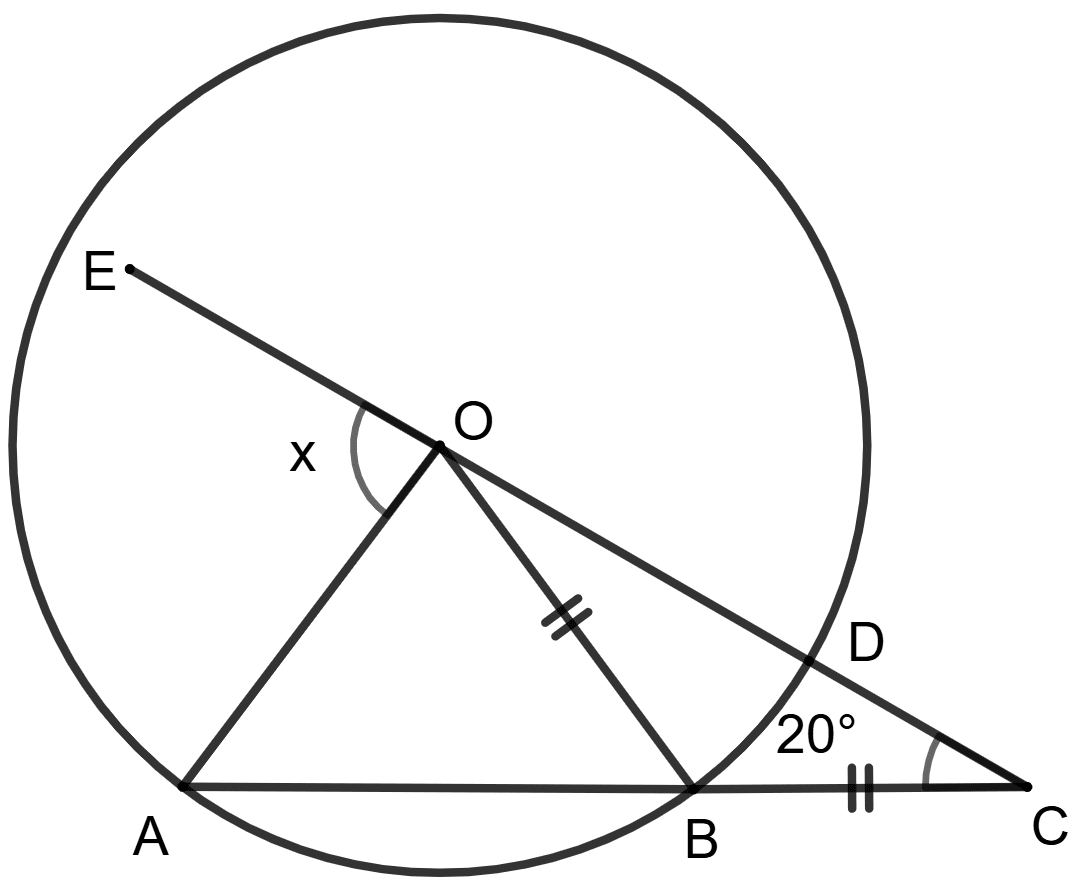
Statement (1) : x = 2 x 20° = 40°
Statement (2) : ∠BOC = 20°.
x = ∠OAB + 20° = ∠OBA + 20° = 40° + 20° = 60°
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Circles
1 Like
Answer
Given,
⇒ OB = OC
⇒ ∠BOC = ∠BCO = 20° (Angles opposite to equal sides of a triangle are always equal)
In △ OBC, using angle sum property,
⇒ ∠OBC + ∠BCO + ∠BOC = 180°
⇒ ∠OBC + 20° + 20° = 180°
⇒ ∠OBC + 40° = 180°
⇒ ∠OBC = 180° - 40°
⇒ ∠OBC = 140°
∠OBC and ∠OBA forms linear pairs of angle.
⇒ ∠OBC + ∠OBA = 180°
⇒ 140° + ∠OBA = 180°
⇒ ∠OBA = 180° - 140°
⇒ ∠OBA = 40°
Since OB = OA (Radii of same circle)
⇒ ∠OBA = ∠OAB = 40° (Angles opposite to equal sides of a triangle are always equal)
Using exterior angle property, the exterior angle of a triangle is equal to the sum of the two opposite interior angles.
In triangle OAC,
⇒ ∠EOA = ∠OAC + ∠OCA
⇒ x = ∠OAB + 20°
⇒ x = ∠OBA + 20° = 40° + 20° = 60°
So, statement 1 is false and statement 2 is true.
Hence, option 4 is the correct option.
Answered By
3 Likes
Related Questions
A circle with center at point O and ∠AOC = 160°.
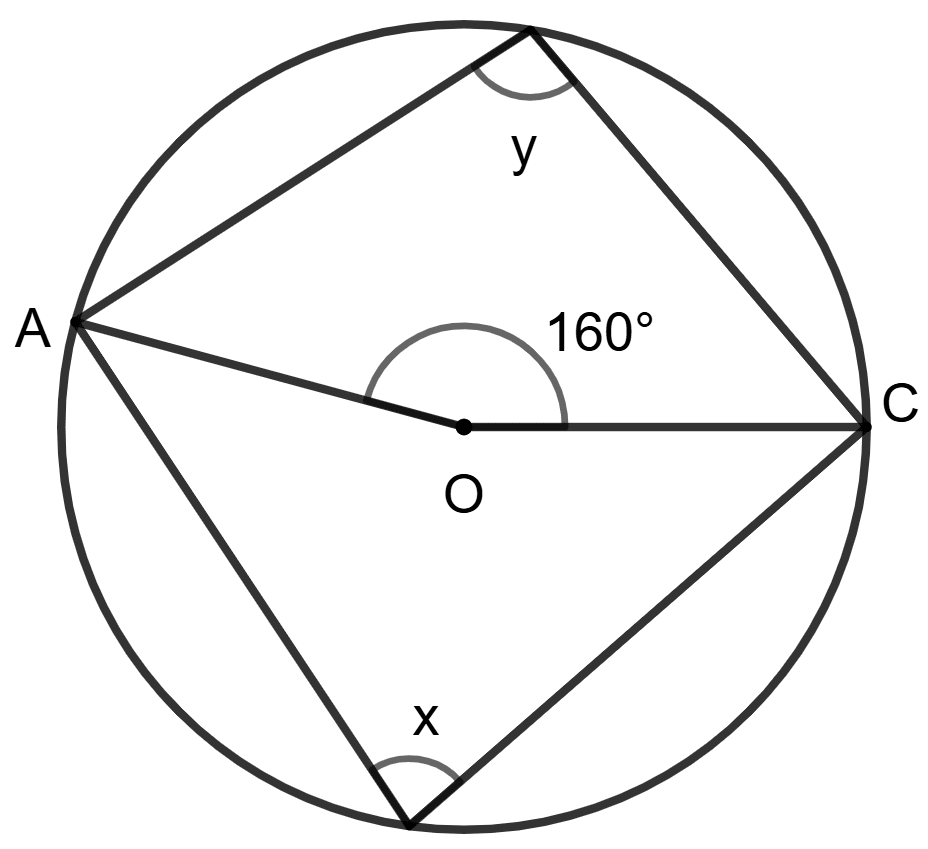
Statement (1) : Angle x = 100° and angle y = 80°.
Statement (2) : The angle, which an arc of a circle subtends at the center of the circle is double the angle which it subtends at any point on the remaining part of the circumference.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
AC is diameter, AE is parallel to BC and ∠BAC = 50°.
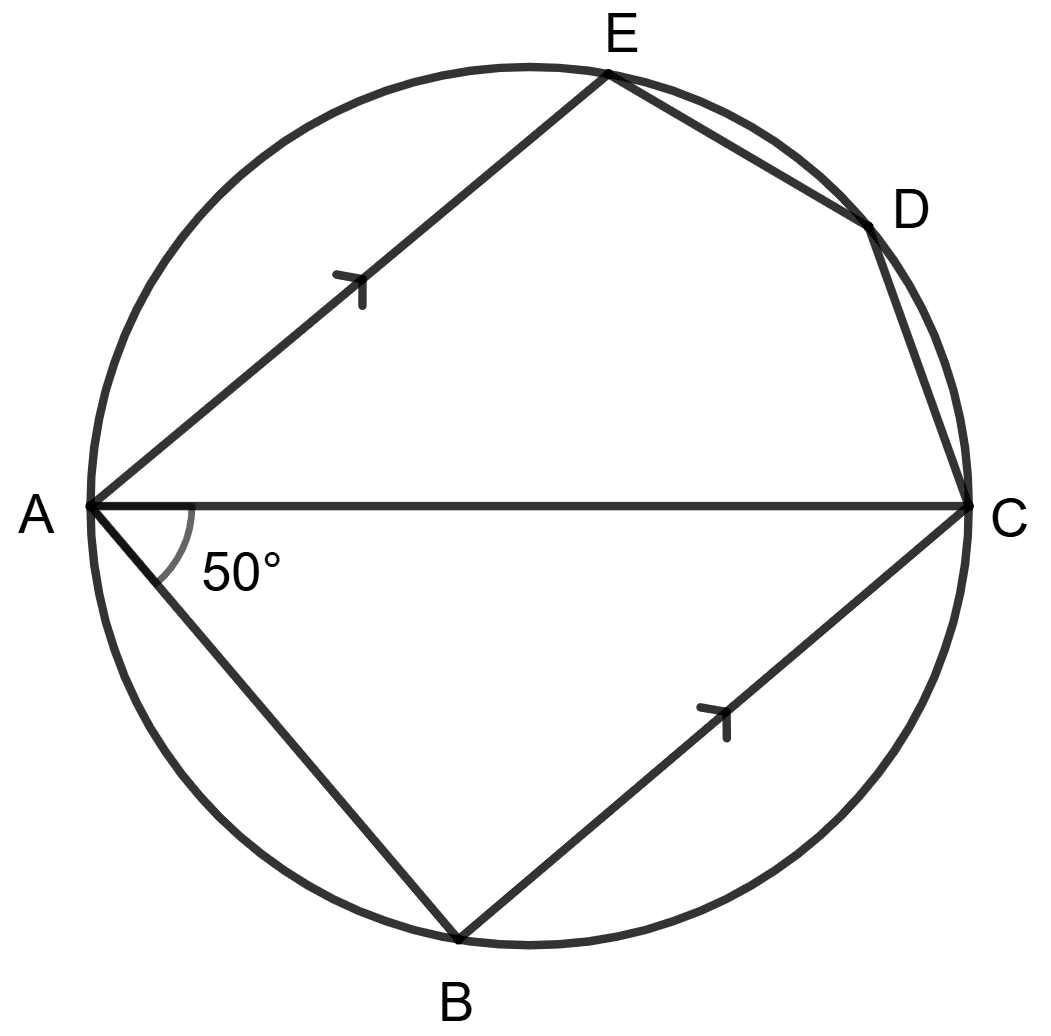
Statement (1) : ∠EDC + 50° = 180°.
Statement (2) : ∠EDC + ∠EAC = 180°.
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
O is the center of the circle and ∠AOC = 120°.
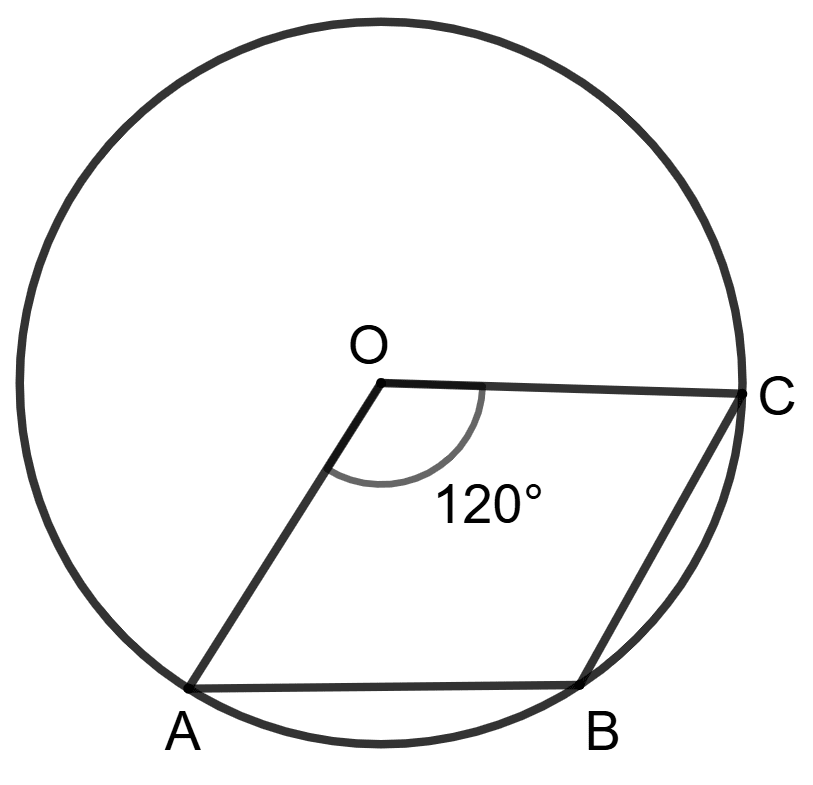
Statement (1) : ∠ABC = 120°
Statement (2) : ∠ABC + ∠ADC = 180° ⇒ ∠ABC + 60° = 180°.
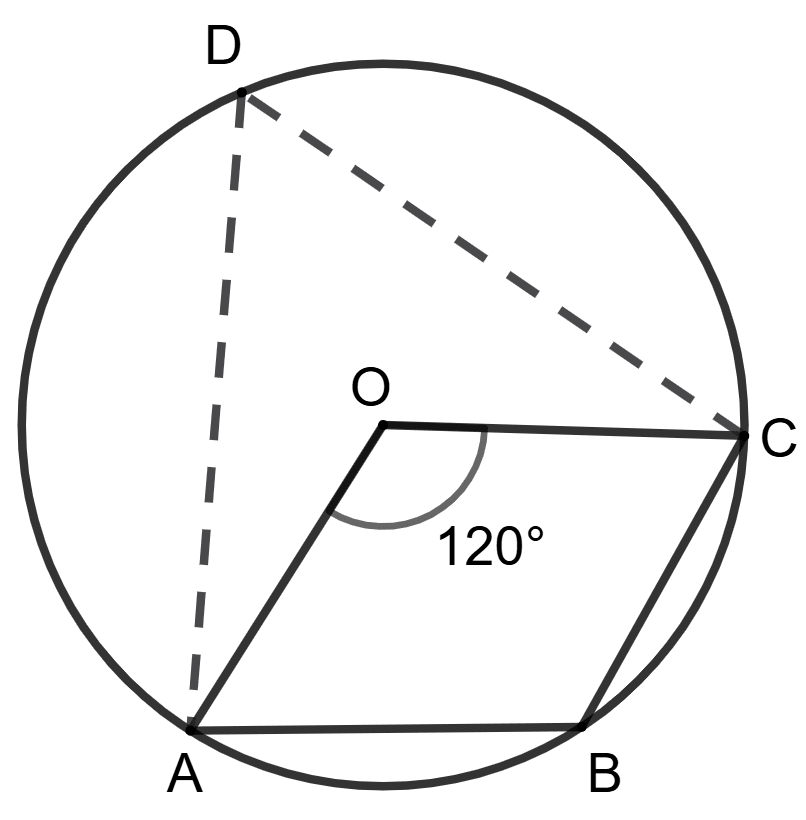
Both statements are true.
Both statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
In the given circle with diameter AB, find the value of x.
