Mathematics
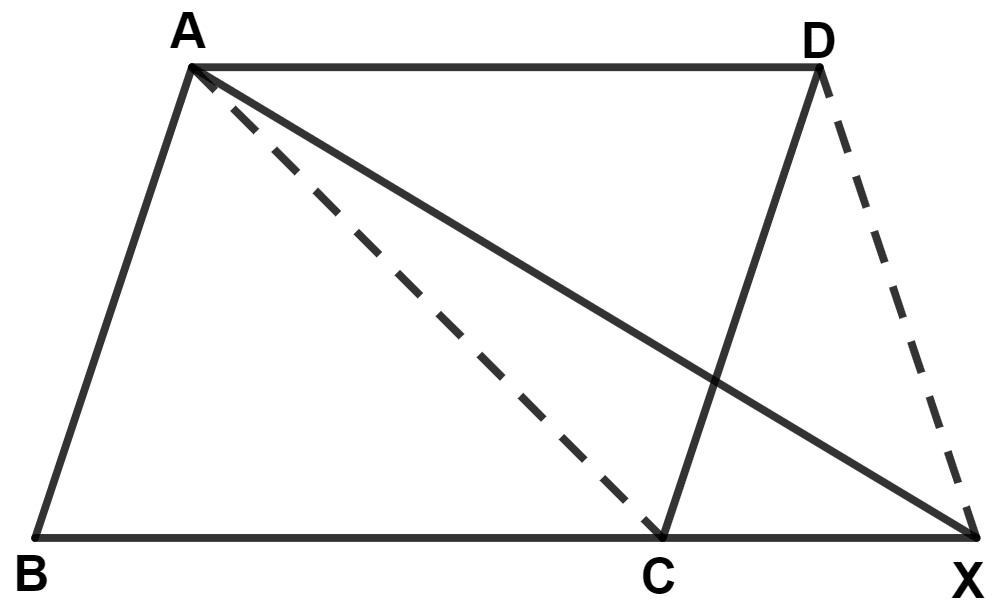
In the given figure, ABCD is a parallelogram. BC is produced to point X. Prove that :
area (△ ABX) = area (quad.ACXD)
Theorems on Area
8 Likes
Answer
Since, ABCD is a parallelogram.
∴ AD // BC (Opposite sides of parallelogram are parallel)
We know that,
Area of triangles on the same base and between the same parallels lines are equal.
△ ABC and △ ADC lie on same base AC and between same parallel lines AD and BC.
∴ Area of △ ABC = Area of △ ACD ……..(1)
△ ACX and △ CXD lie on same base CX and between same parallel lines AD and BX.
∴ Area of △ ACX = Area of △ CXD ……..(2)
From figure,
⇒ Area of △ ABX = Area of △ ABC + Area of △ ACX
⇒ Area of △ ABX = Area of △ ACD + Area of △ CXD [From equation (1) and (2)]
⇒ Area of △ ABX = Area of quadrilateral ACXD.
Hence, proved that area (△ ABX) = area (quad.ACXD).
Answered By
6 Likes
Related Questions
ABCD is a trapezium with AB // DC. A line parallel to AC intersects AB at point M and BC at point N. Prove that :
area of △ ADM = area of △ ACN.
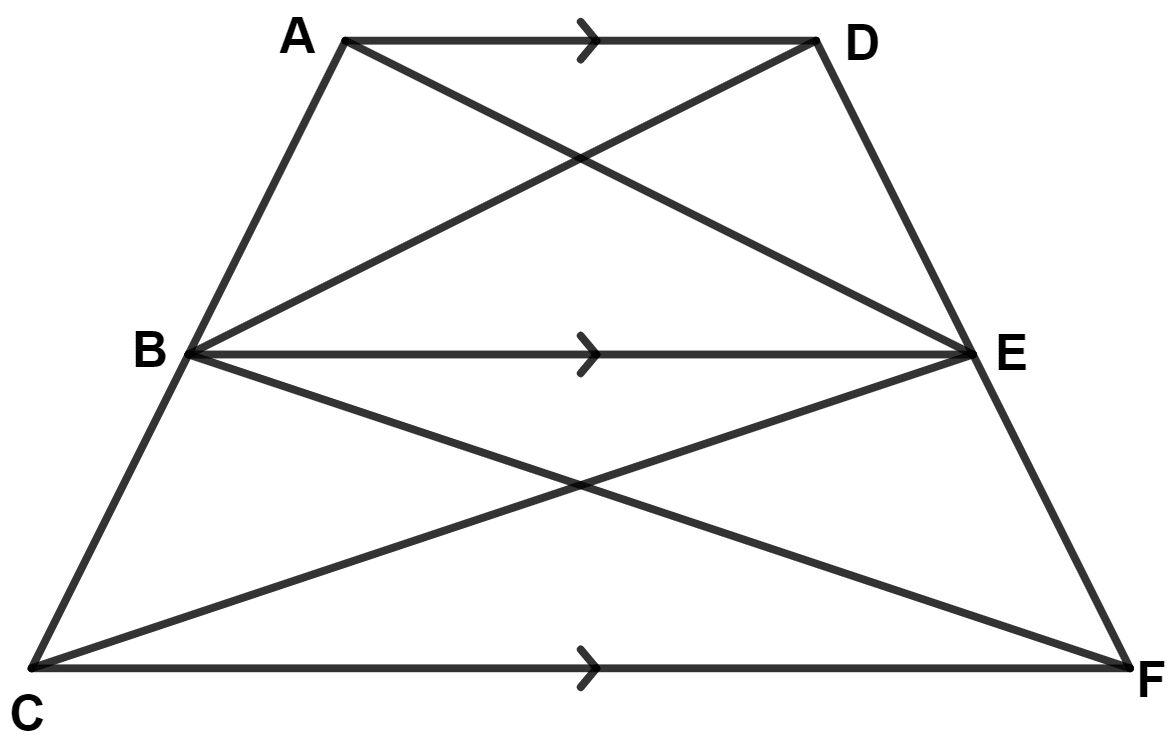
In the given figure, AD // BE // CF. Prove that :
area (△ AEC) = area (△ DBF)
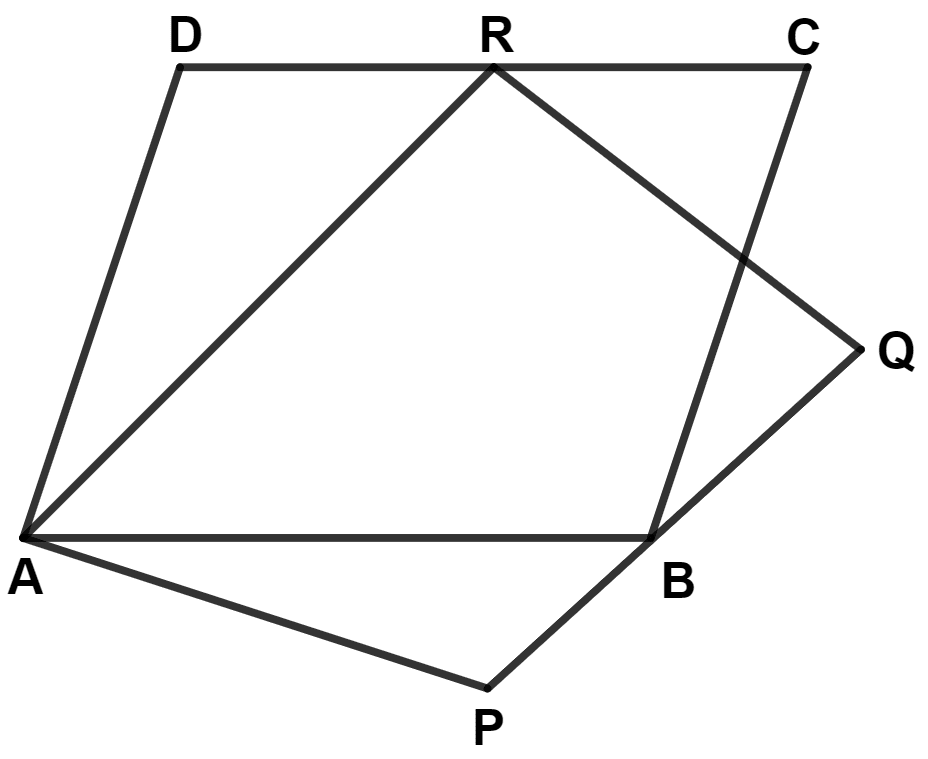
The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
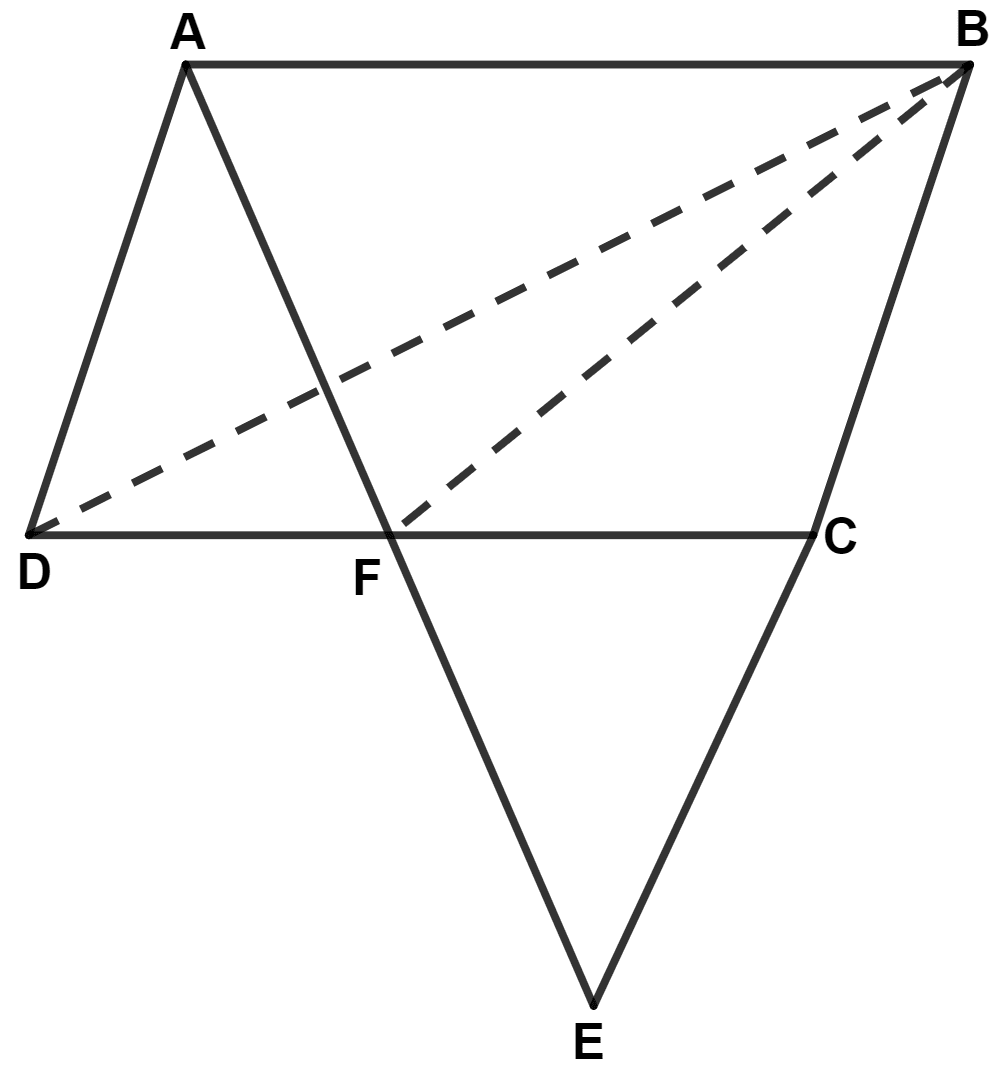
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F. If ar.(△ DFB) = 30 cm2; find the area of parallelogram.