Mathematics
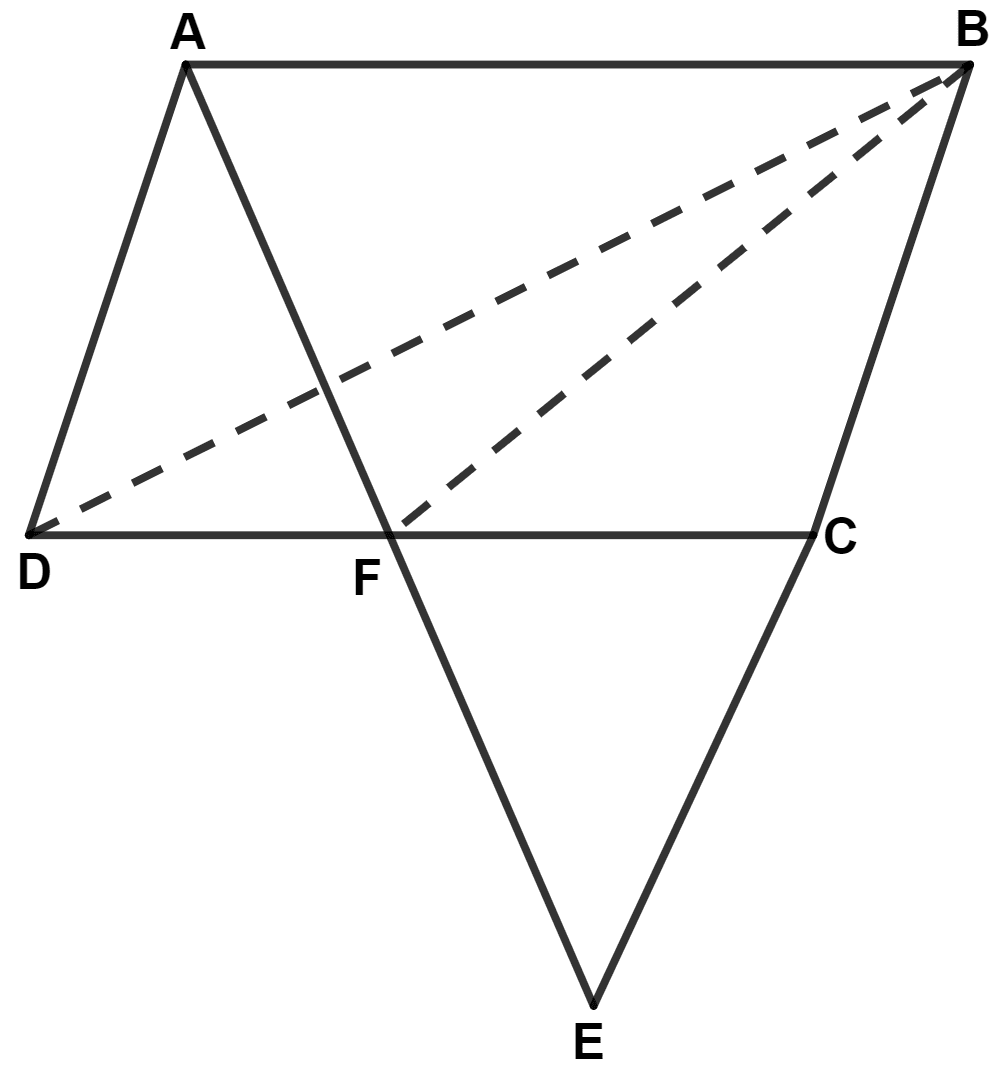
ABCD is a parallelogram in which BC is produced to E such that CE = BC and AE intersects CD at F. If ar.(△ DFB) = 30 cm2; find the area of parallelogram.
Theorems on Area
6 Likes
Answer
We know that,
Area of triangles on the same base and between the same parallel lines are equal.
△ ADF and △ DFB lie on same base DF and between same parallel lines AB and DC.
∴ Area of △ ADF = Area of △ DFB = 30 cm2
By converse of mid-point theorem,
If a line is drawn through the midpoint of one side of a triangle, and parallel to the other side, it bisects the third side.
In △ ABE,
C is the mid-point of BE and CF || AB.
∴ F is the mid-point of AE. (By converse of mid-point theorem)
∴ EF = AF.
In △ ADF and △ EFC,
⇒ ∠AFD = ∠EFC (Vertically opposite angles are equal)
⇒ EF = AF (Proved above)
⇒ ∠DAF = ∠CEF (Alternate interior angles are equal)
∴ △ ADF ≅ △ EFC (By A.S.A. axiom)
We know that,
Area of congruent triangles are equal.
∴ Area of △ EFC = Area of △ ADF = 30 cm2.
In △ BFE,
Since, C is the mid-point of BE.
∴ CF is the mid-point of median of triangle.
We know that,
Median of triangle divides it into two triangles of equal areas.
∴ Area of △ BFC = Area of △ EFC = 30 cm2.
From figure,
⇒ Area of △ BDC = Area of △ BDF + Area of △ BFC
⇒ Area of △ BDC = 30 + 30 = 60 cm2.
We know that,
The area of triangle is half that of a parallelogram on the same base and between the same parallels.
From figure,
|| gm ABCD and △ BDC lies on same base DC and between same parallel lines AB and DC.
∴ Area of △ BDC = Area of || gm ABCD
⇒ Area of || gm ABCD = 2 × Area of △ BDC
⇒ Area of || gm ABCD = 2 × 60 = 120 cm2.
Hence, area of || gm ABCD = 120 cm2.
Answered By
4 Likes
Related Questions
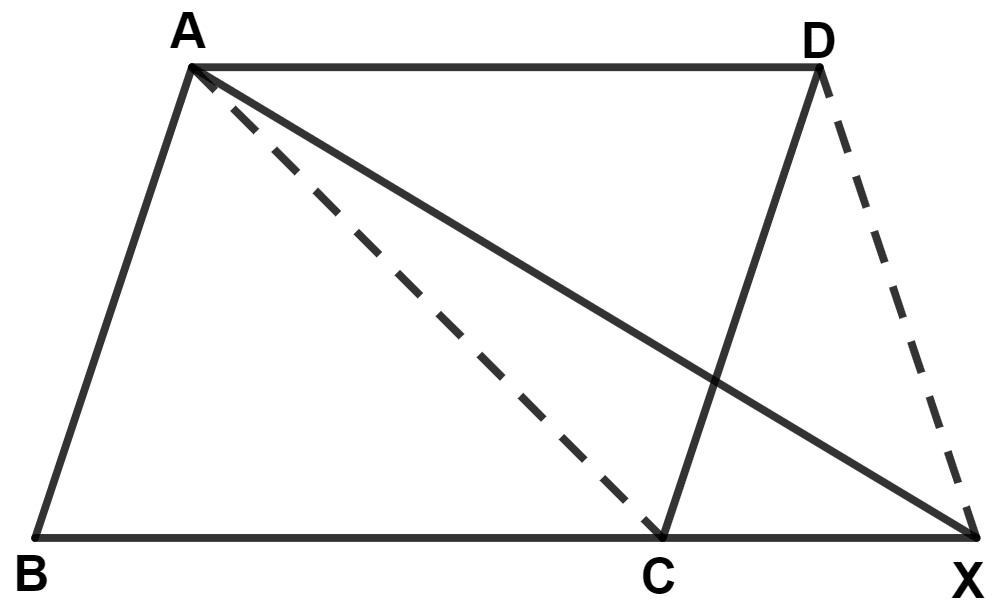
In the given figure, ABCD is a parallelogram. BC is produced to point X. Prove that :
area (△ ABX) = area (quad.ACXD)
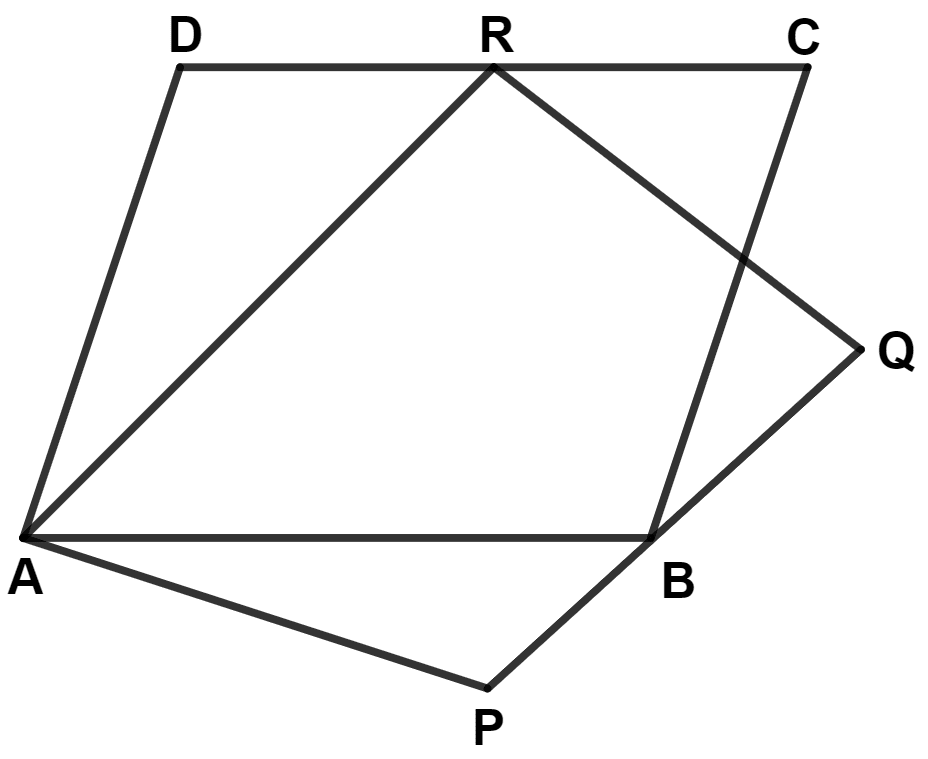
The given figure shows parallelograms ABCD and APQR. Show that these parallelograms are equal in area.
The following figure shows a triangle ABC in which P, Q and R are mid-points of sides AB, BC and CA respectively. S is mid-point of PQ. Prove that :
ar.(△ ABC) = 8 × ar.(△ QSB)
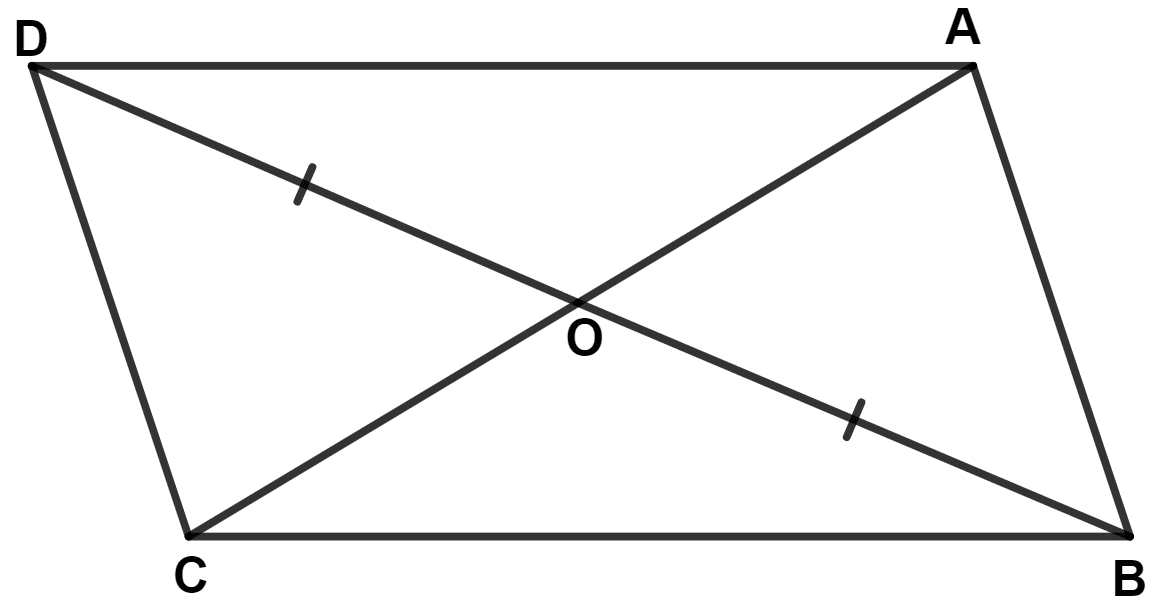
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB // DC, prove that :
(i) Area of (△ DOC) = Area of (△ AOB)
(ii) Area of (△ DCB) = Area of (△ ACB)
(iii) ABCD is a parallelogram.