Mathematics
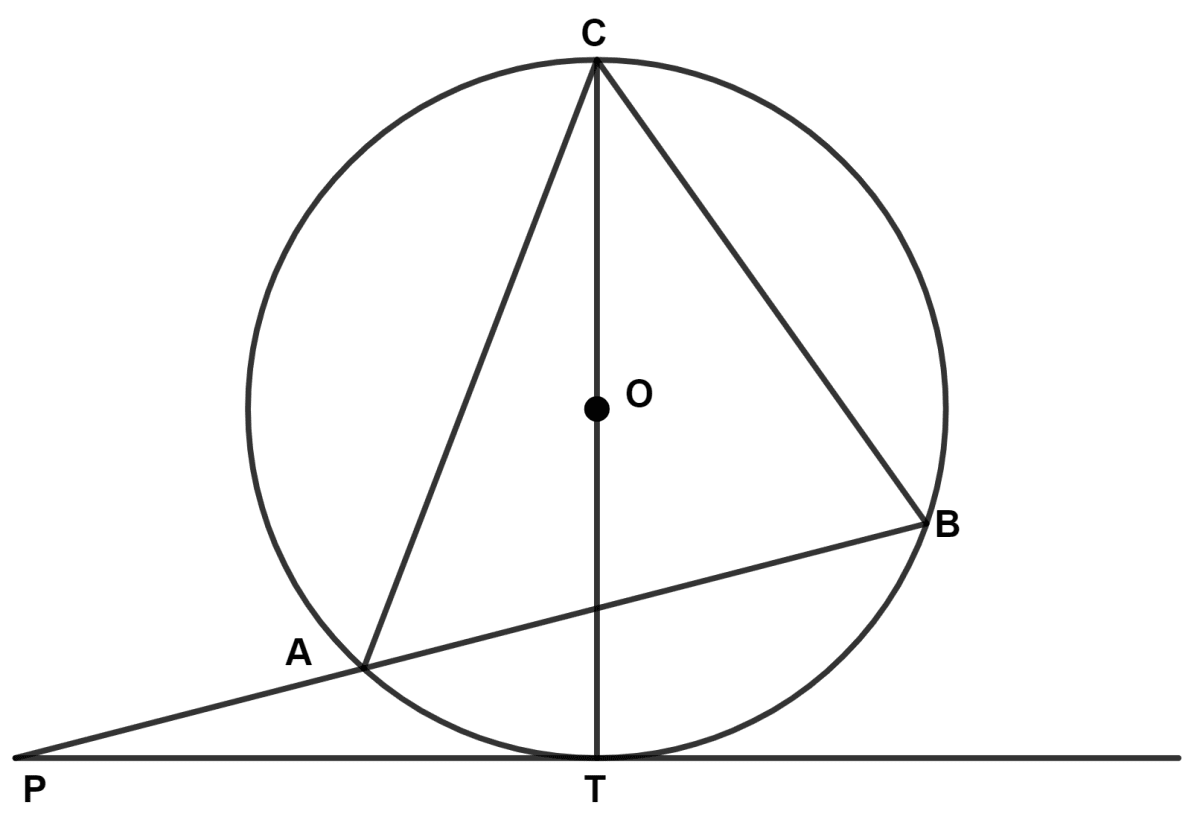
In the given figure, angle ABC = 70° and angle ACB = 50°. Given, O is the centre of the circle and PT is the tangent to the circle. Then calculate the following angles
(a) ∠CBT
(b) ∠BAT
(c) ∠PBT
(d) ∠APT
Answer
Join AT and BT.
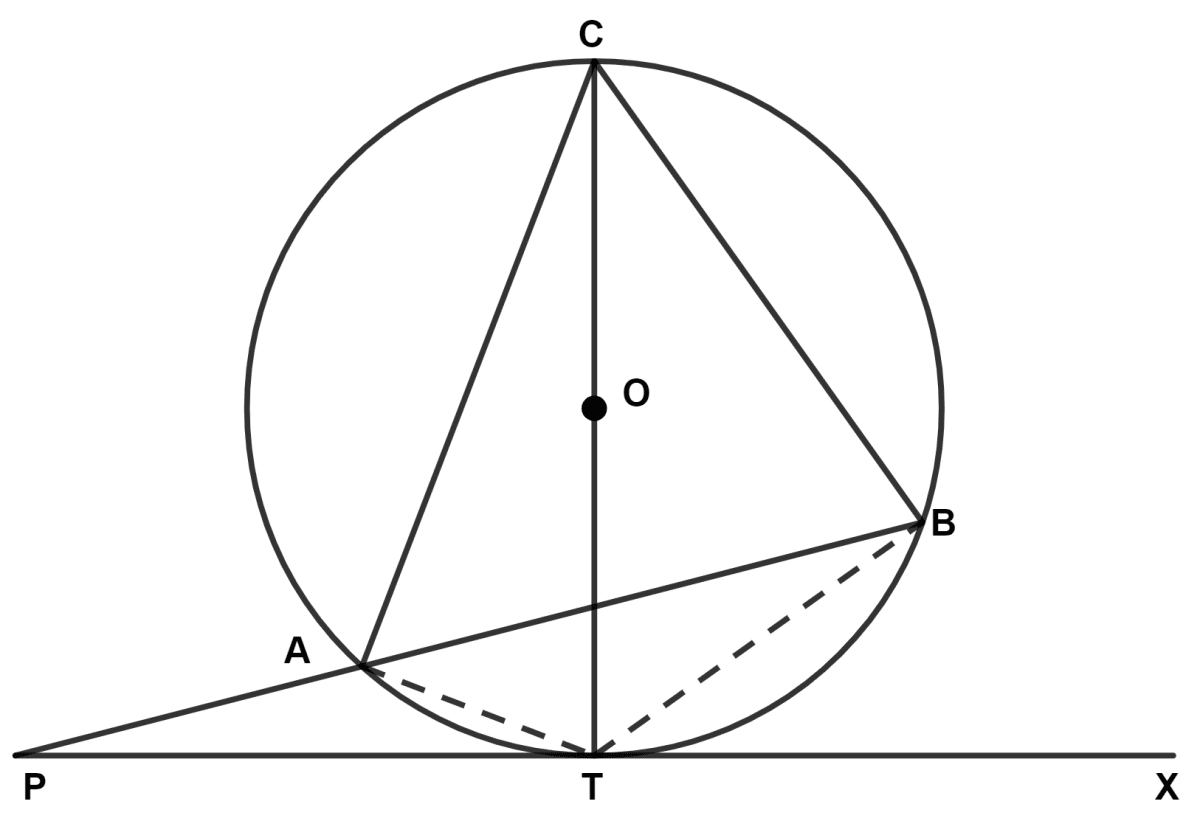
(a) We know that,
Angle in a semicircle is a right angle.
∴ ∠CBT = 90°.
Hence, ∠CBT = 90°.
(b) In cyclic quadrilateral ATBC,
⇒ ∠CBT + ∠CAT = 180° (∵ Sum of opposite angles of a cyclic quadrilateral = 180°)
⇒ 90° + ∠CAT = 180°
⇒ ∠CAT = 180° - 90° = 90°.
In △ABC,
⇒ ∠CBA + ∠CAB + ∠ACB = 180° [By angle sum property of triangle]
⇒ 70° + ∠CAB + 50° = 180°
⇒ ∠CAB + 120° = 180°
⇒ ∠CAB = 180° - 120°
⇒ ∠CAB = 60°.
From figure,
∠BAT = ∠CAT - ∠CAB = 90° - 60° = 30°.
Hence, ∠BAT = 30°.
(c) From figure,
∠BTX = ∠BAT = 30° [Angle in same segment are equal]
∠PBT = ∠CBT - ∠CBA = 90° - 70° = 20°.
Hence, ∠PBT = 20°.
(d) Since, ∠PTB and ∠BTX are linear pairs.
⇒ ∠PTB = 180° - ∠BTX = 180° - 30° = 150°.
In △PBT,
⇒ ∠PBT + ∠PTB + ∠APT = 180° [By angle sum property of triangle]
⇒ 20° + 150° + ∠APT = 180°
⇒ ∠APT + 170° = 180°
⇒ ∠APT = 180° - 170°
⇒ ∠APT = 10°.
Hence, ∠APT = 10°.
Related Questions
In the given figure (not drawn to scale), BC is parallel to EF, CD is parallel to FG, AE : EB = 2 : 3, ∠BAD = 70°, ∠ACB = 105°, ∠ADC = 40° and AC is bisector of ∠BAD.
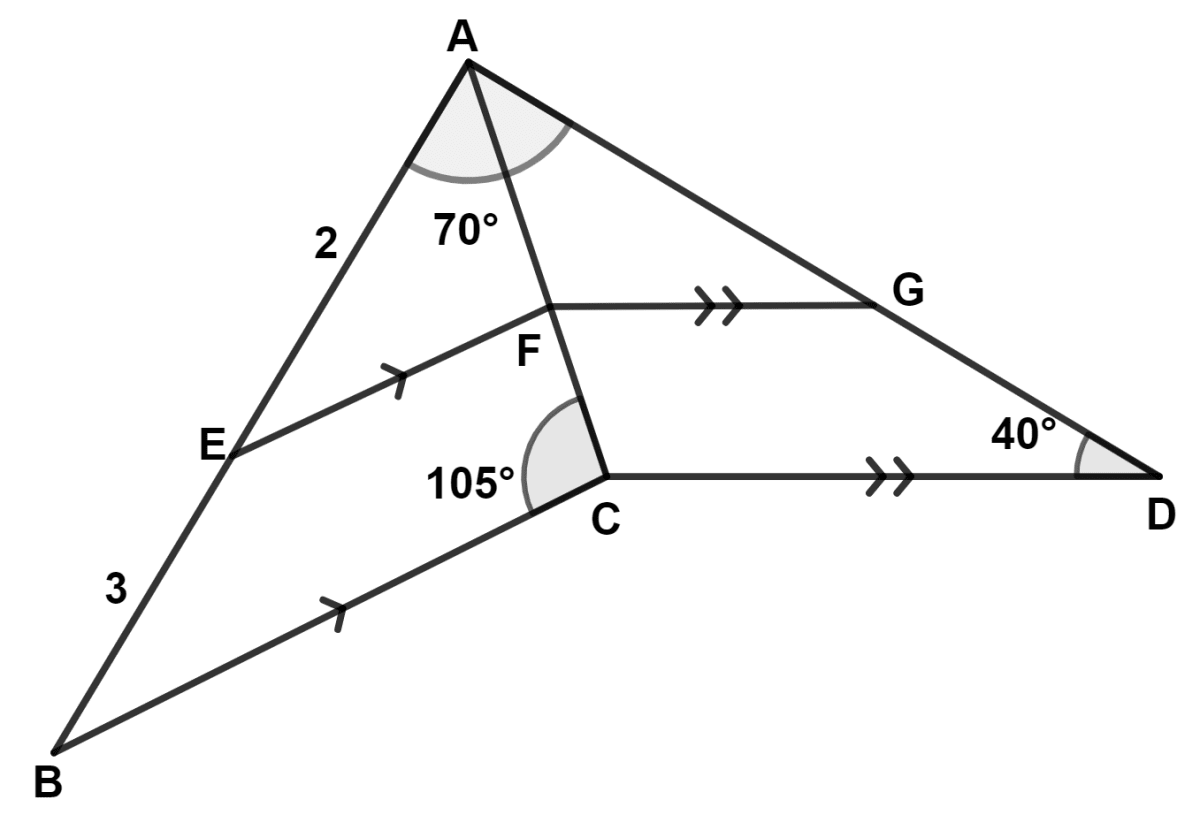
(a) Prove Δ AEF ~ Δ AGF
(b) Find :
(i) AG : AD
(ii) area of Δ ACB: area Δ ACD
(iii) area of quadrilateral ABCD: area of Δ ACB.
(a) Construct a triangle ABC such that BC = 8 cm, AC = 10 cm and ∠ABC = 90°.
(b) Construct an incircle to this triangle. Mark the centre as I.
(c) Measure and write the length of the in-radius.
(d) Measure and write the length of the tangents from vertex C to the incircle.
(e) Mark points P, Q and R where the incircle touches the sides AB, BC, and AC of the triangle respectively. Write the relationship between ∠RIQ and ∠QCR.
(Use a ruler and a compass for this question.)
The daily wages of workers in a construction unit were recorded as follows :
Class marks (Wages) No. of workers 425 6 475 12 525 15 575 17 625 7 675 13 Form a frequency distribution table with class intervals and find modal wage by plotting a histogram.