Mathematics
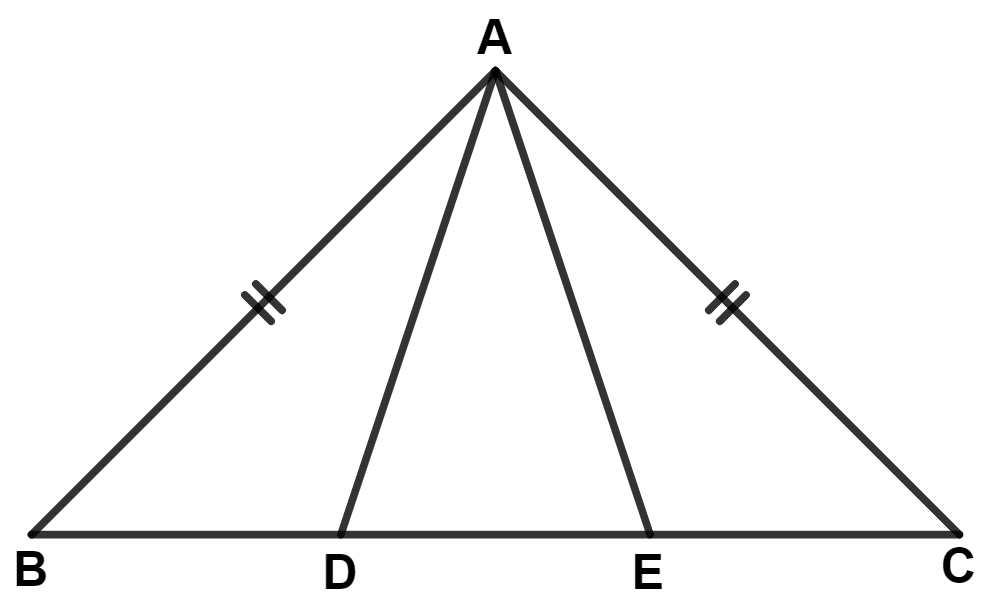
In the given figure; BE = DC, then :
AD = DC
AE = BE
AD = AE
∠ABE = ∠DAC
Triangles
24 Likes
Answer
From figure,
⇒ AB = AC
∴ ∠B = ∠C (Angles opposite to equal sides are equal)
Given,
⇒ BE = DC
⇒ BD + DE = DE + EC
⇒ BD = EC.
In △ ABD and △ AEC,
⇒ BD = EC (Proved above)
⇒ AB = AC (Given)
⇒ ∠B = ∠C (Proved above)
∴ △ ABD ≅ △ AEC (By S.A.S. axiom)
We know that,
Corresponding parts of congruent triangle are equal.
∴ AD = AE.
Hence, Option 3 is the correct option.
Answered By
12 Likes
Related Questions
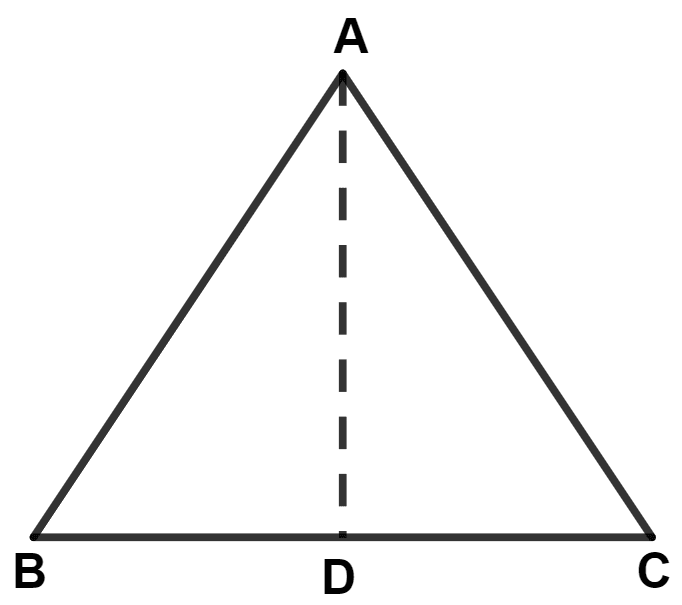
In the given figure, AD ⊥ BC and AB = AC, then :
△ ABD ≇ △ ACD
BD = CD
∠BAC = 90°
∠CAD = 45°
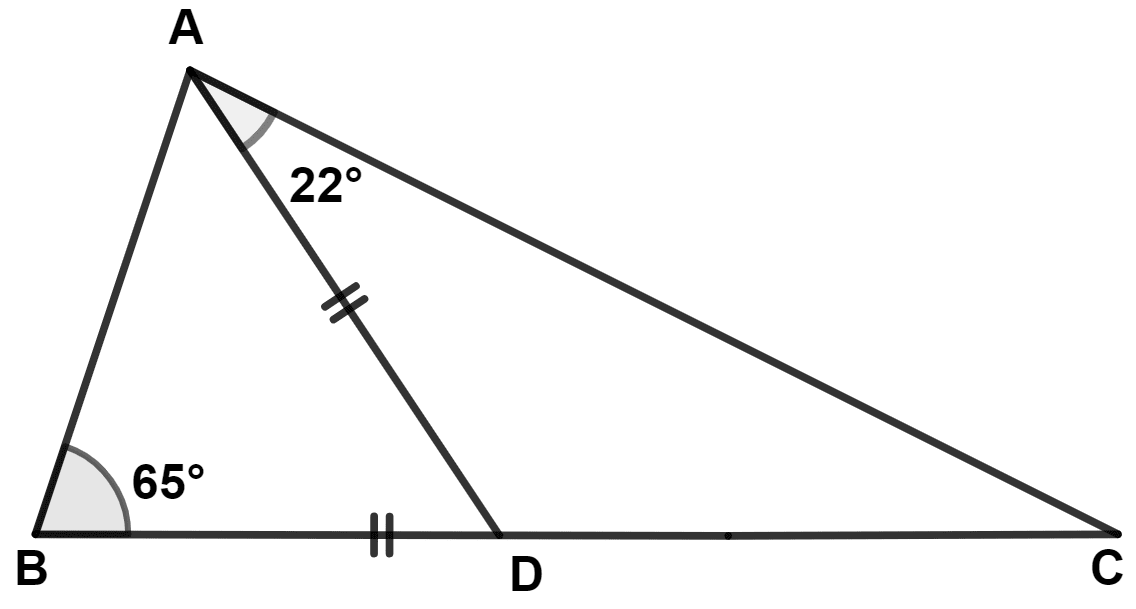
In the given figure, AD = BD, then angle ACD is :
43°
22°
65°
28°
In △ ABC and △ PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q; then triangles are :
isosceles but not congruent
isosceles and congruent
congruent but not isosceles
neither isosceles nor congruent.
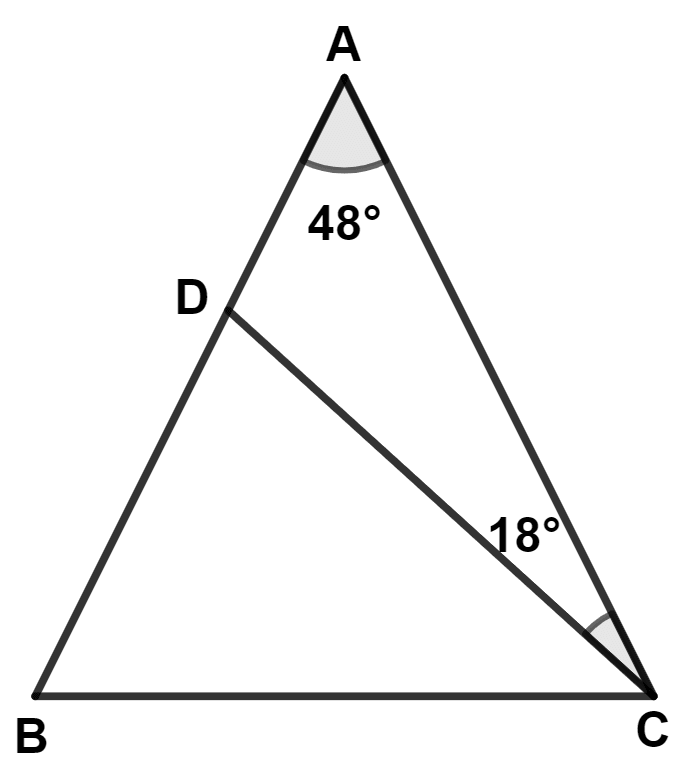
In the figure alongside,
AB = AC
∠A = 48° and
∠ACD = 18°.
Show that : BC = CD.