Mathematics
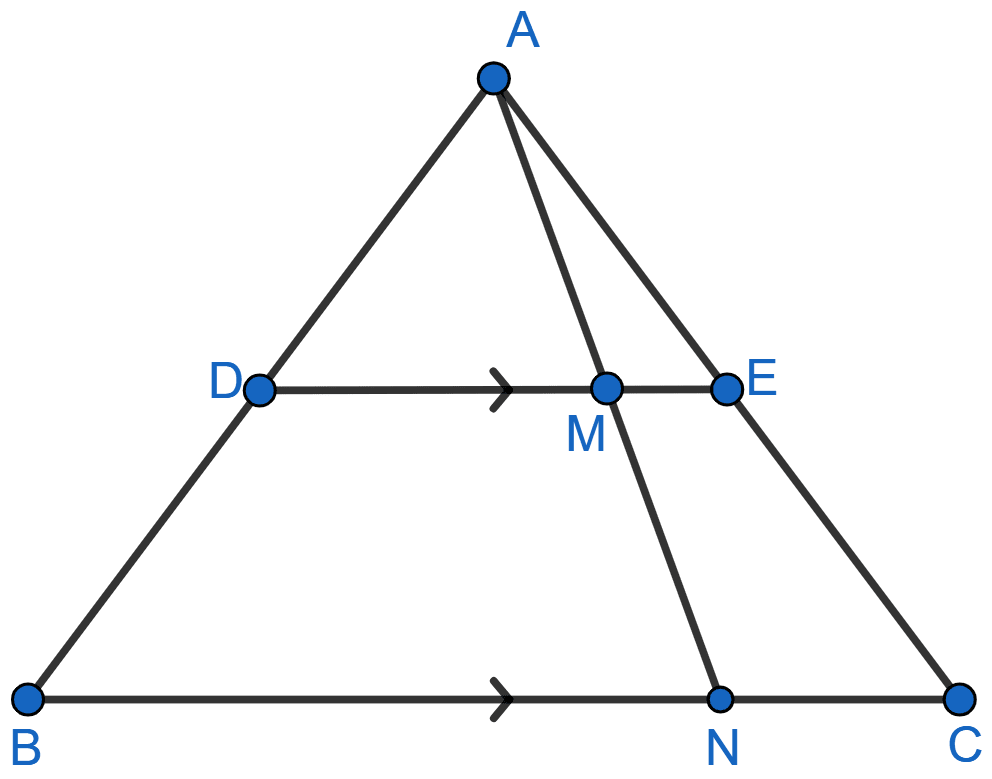
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
Similarity
72 Likes
Answer
(i) In ΔAME and ΔANC,
⇒ ∠AME = ∠ANC [Since DE || BC so, ME || NC and AN is transversal]
⇒ ∠MAE = ∠NAC [Common angle]
∴ ∆AME ~ ∆ANC [By AA]
In ΔADM and ΔABN,
⇒ ∠ADM = ∠ABN [Since DE || BC so, DM || BN and AB is transversal]
⇒ ∠DAM = ∠BAN [Common angle]
∴ ∆ADM ~ ∆ABN [By AA]
In ΔADE and ΔABC,
⇒ ∠ADE = ∠ABC [Since DE || BC and AB is transversal]
⇒ ∠AED = ∠ACB [Since DE || BC and AC is transversal]
∴ ∆ADE ~ ∆ABC [By AA]
Hence, ∆ADM ~ ∆ABN, ∆AME ~ ∆ANC and ∆ADE ~ ∆ABC.
(ii) Since, ∆AME ~ ∆ANC
We know that,
Corresponding sides of similar triangles are proportional.
Since, ∆ADE ~ ∆ABC [Proved above]
We know that,
Corresponding sides of similar triangles are proportional.
……… (1)
Also, ∆ADM ~ ∆ABN [Proved above]
Hence, ME = 3.75 cm and DM = 15 cm.
Answered By
38 Likes
Related Questions
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
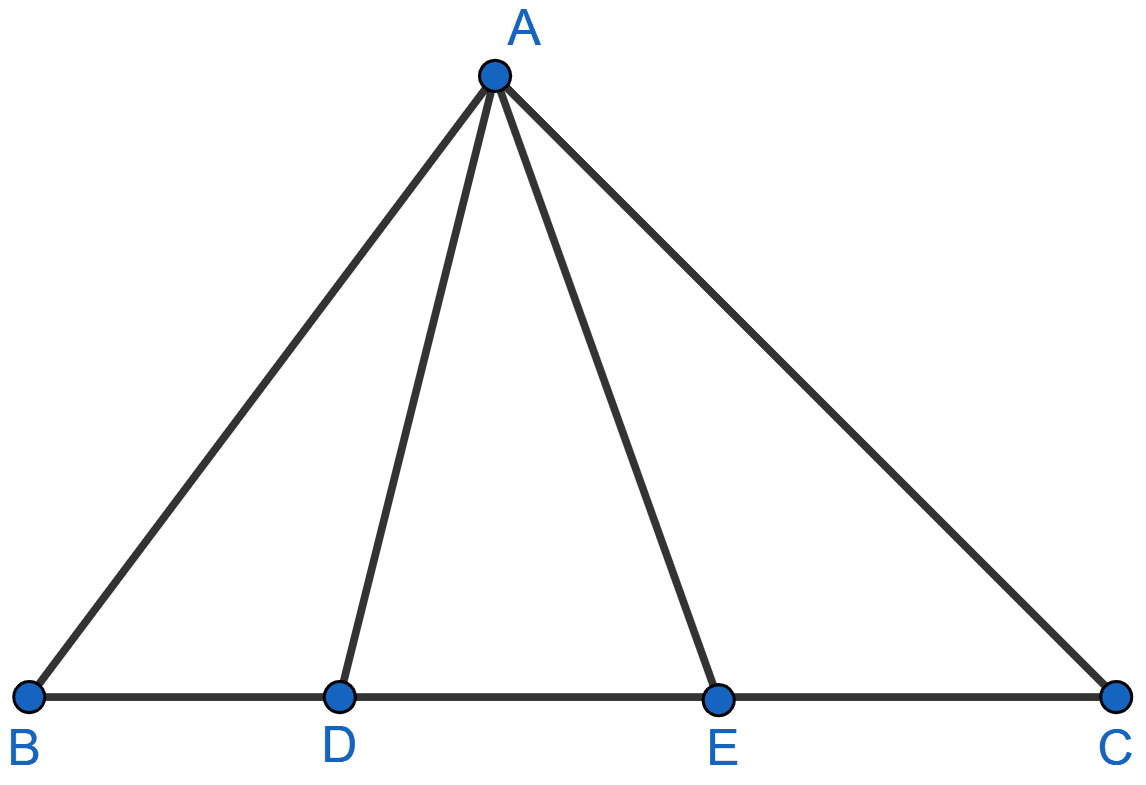
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.