Mathematics
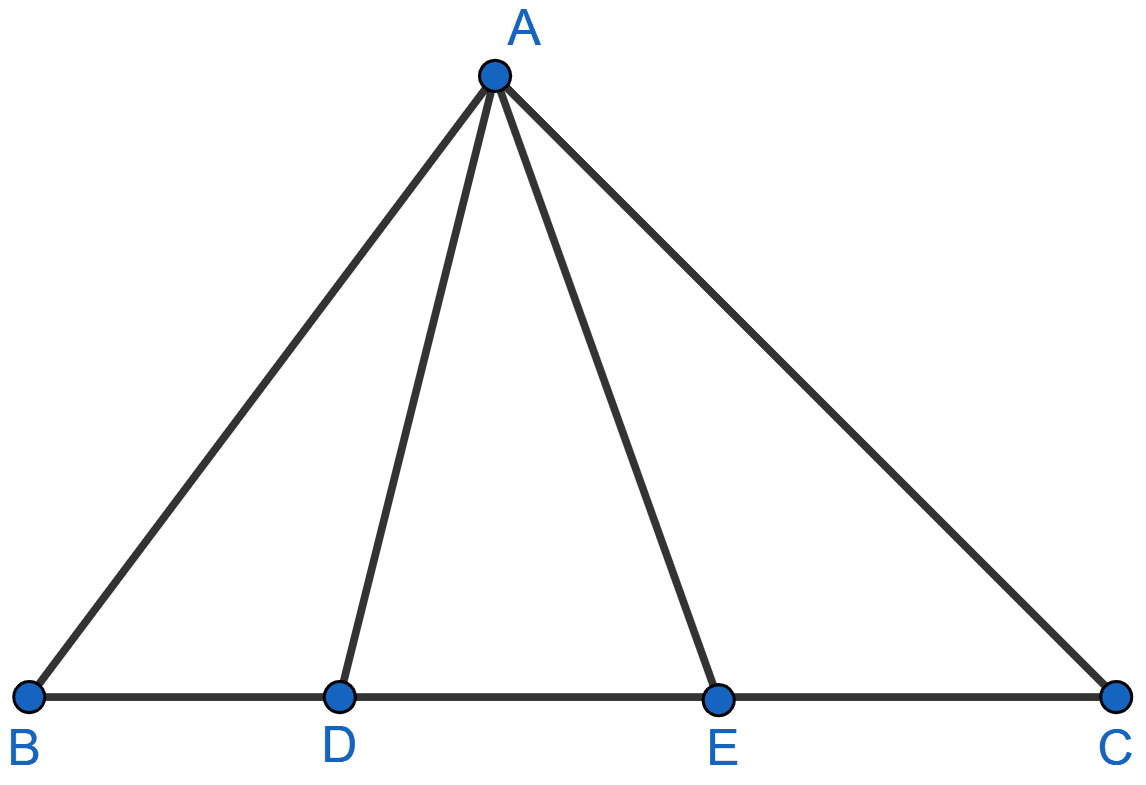
In the given figure, AD = AE and AD2 = BD x EC. Prove that: triangles ABD and CAE are similar.
Similarity
49 Likes
Answer
From figure,
⇒ ∠ADE = ∠AED [Angles opposite to equal sides of a triangle are equal].
⇒ 180° - ∠ADE = 180° - ∠AED
⇒ ∠ADB = ∠AEC
Given,
⇒ AD2 = BD x EC
⇒ AD x AD = BD x EC
⇒ AD x AE = BD x EC
⇒
∴ △ABD ~ △CAE [By SAS]
Hence, proved that △ABD ~ △CAE.
Answered By
28 Likes
Related Questions
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that :
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
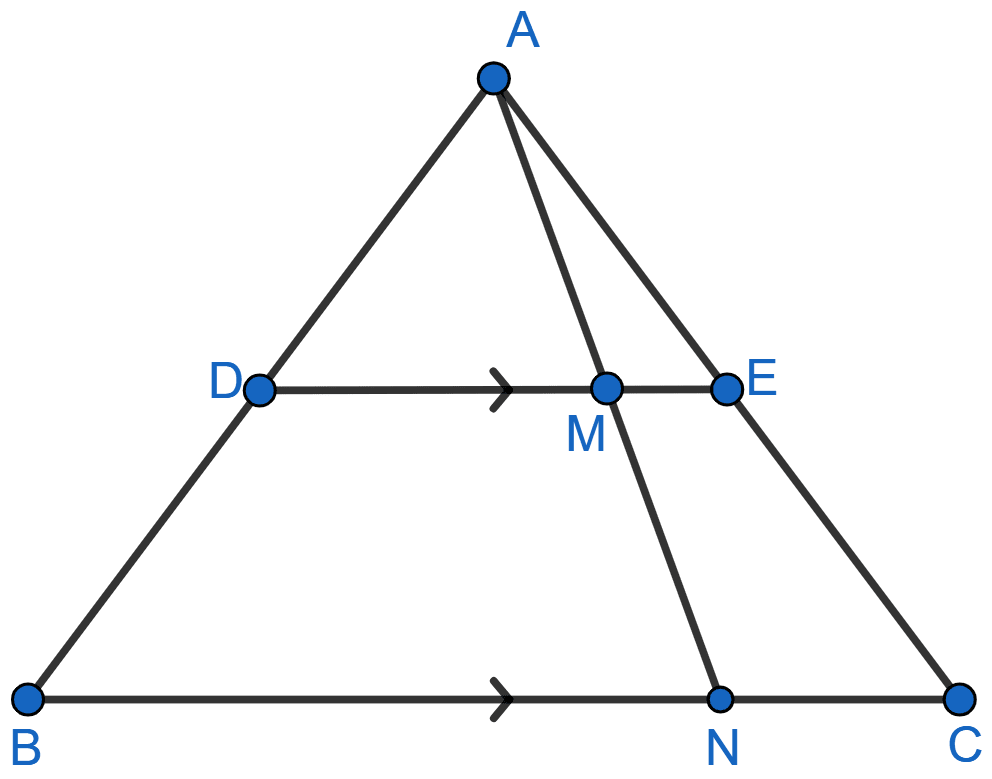
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find the lengths of ME and DM.
State, true or false:
(i) Two similar polygons are necessarily congruent.
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that: CA2 = CB x CD.