Mathematics
In the given figure, the value of AB × CD is :
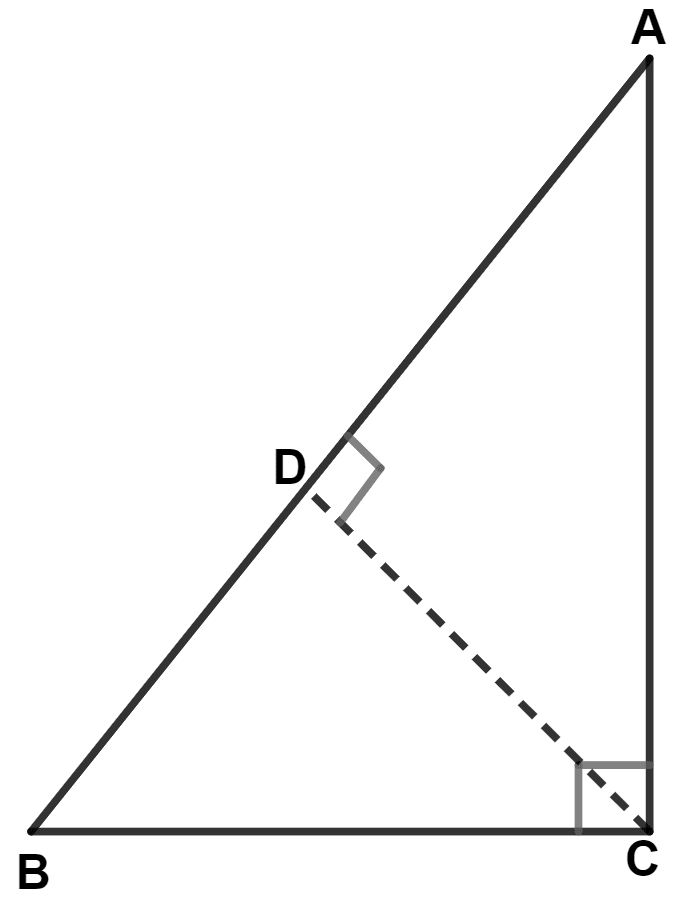
AC × BC
AC × CD
AC × AB
AC2 + BC2
Pythagoras Theorem
23 Likes
Answer
By formula,
⇒ Area of triangle = × base × height
From figure,
⇒ Area of △ ABC = × AB × CD ………(1)
⇒ Area of △ ABC = × BC × AC ………(2)
From equations (1) and (2), we get :
⇒ × AB × CD = × BC × AC
⇒ AB × CD = BC × AC.
Hence, Option 1 is the correct option.
Answered By
13 Likes
Related Questions
In △ ABC, ∠C = 90° and AC = BC, then AB2 is equal to :
AC2
2AC2
BC2
2BC2 - AC2
In the given diagram, AE2 + BD2 is equal to :
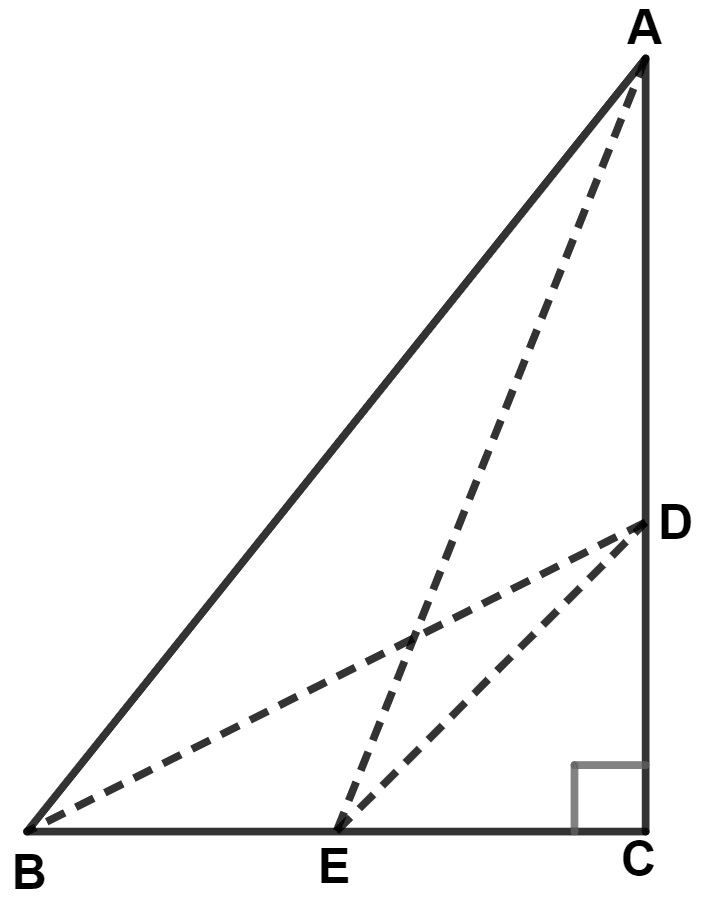
AB2 - DE2
DE2 - AB2
AB2 + DE2
DE × AB
ABC is an isosceles triangle right-angled at C. Then 2AC2 is equal to :
BC2
AC2
AC2 - BC2
AB2
In the figure, given below, AD ⊥ BC. Prove that :
c2 = a2 + b2 - 2ax.
