Mathematics
ABC is an isosceles triangle right-angled at C. Then 2AC2 is equal to :
BC2
AC2
AC2 - BC2
AB2
Pythagoras Theorem
13 Likes
Answer

Since, ABC is an isosceles triangle right-angled at C.
∴ ∠A = ∠B
∴ BC = AC [Sides opposite to equal angles are equal] ……..(1)
In right-angled △ ABC,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ AB2 = AC2 + BC2
⇒ AB2 = AC2 + AC2 [From equation (1)]
⇒ AB2 = 2AC2.
Hence, Option 4 is the correct option.
Answered By
9 Likes
Related Questions
In the given diagram, AE2 + BD2 is equal to :
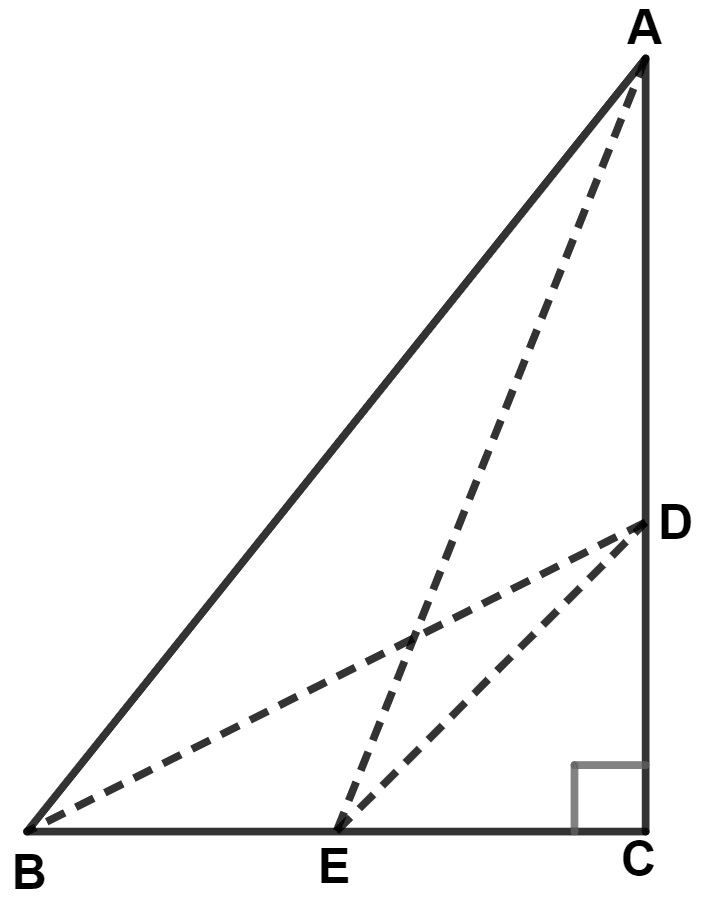
AB2 - DE2
DE2 - AB2
AB2 + DE2
DE × AB
In the given figure, the value of AB × CD is :
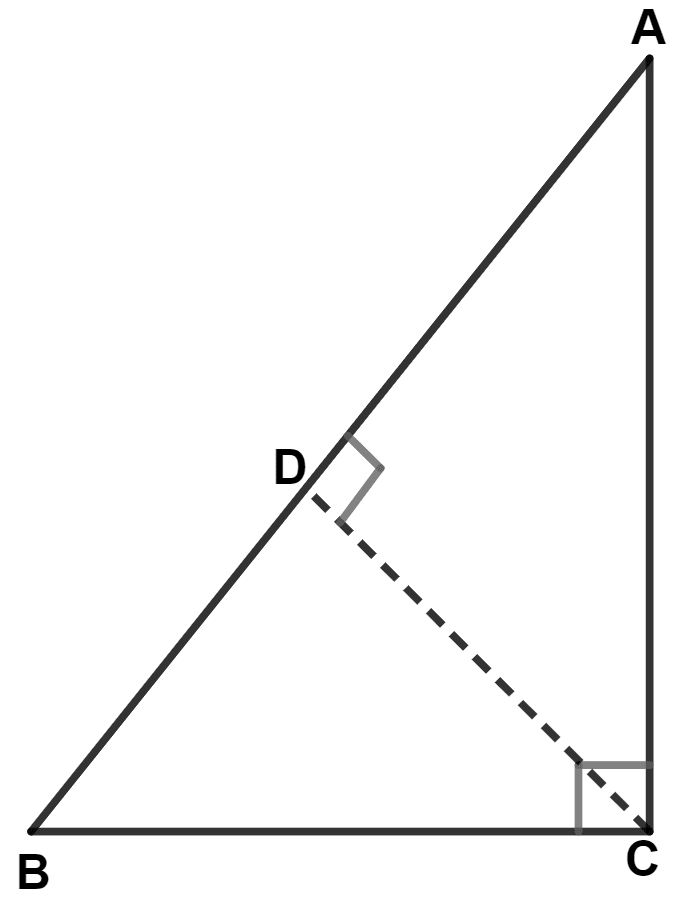
AC × BC
AC × CD
AC × AB
AC2 + BC2
In the figure, given below, AD ⊥ BC. Prove that :
c2 = a2 + b2 - 2ax.

In equilateral △ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.