In triangle ABC; angle A = 90°, side AB = x cm, AC = (x + 5) cm and area = 150 cm². Find the sides of the triangle.

Δ ABC is shown in the figure below:

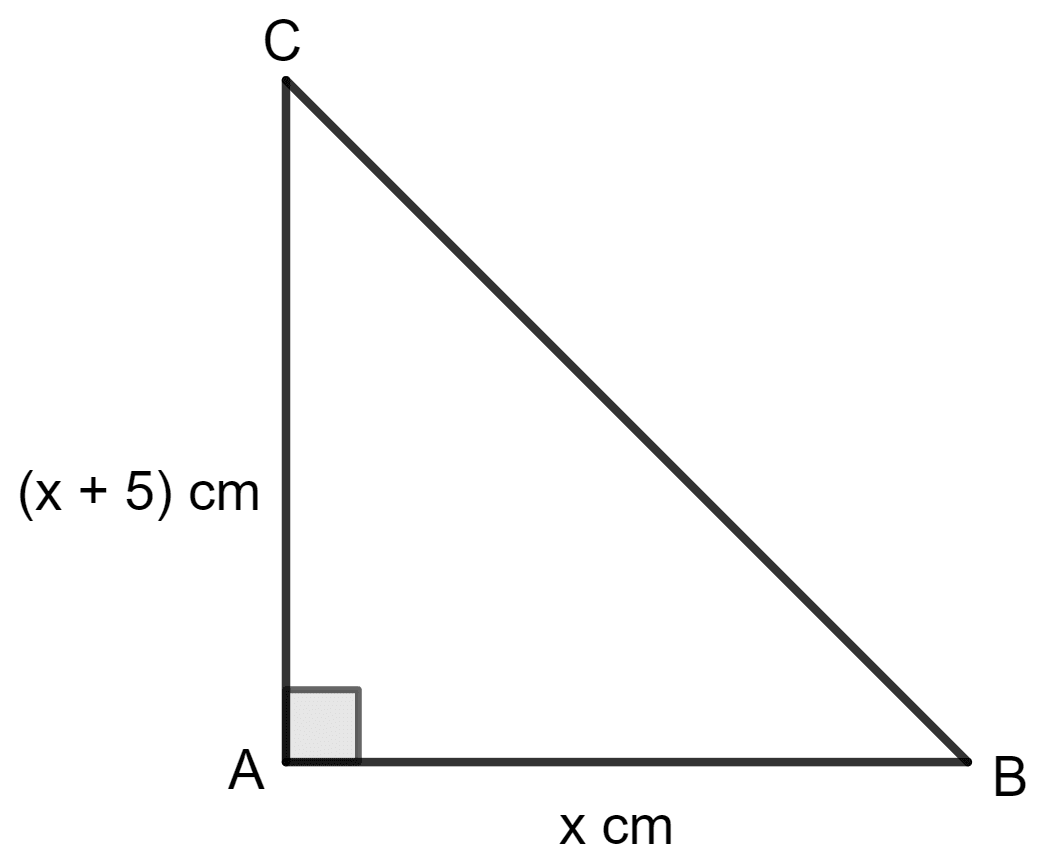
Given:

Area = 150 cm²

Area = $\dfrac{1}{2} \times$ base $\times$ height

$⇒ 150 = \dfrac{1}{2} \times x \times (x + 5)\\[1em] ⇒ 150 \times 2 = x^2 + 5x\\[1em] ⇒ 300 = x^2 + 5x\\[1em] ⇒ x^2 + 5x - 300 = 0\\[1em] ⇒ x^2 + 20x - 15x - 300 = 0\\[1em] ⇒ x(x + 20) - 15(x + 20) = 0\\[1em] ⇒ (x + 20)(x - 15) = 0\\[1em] ⇒ x = -20 \text{ or } 15$

Since length cannot be negative, AB = 15 cm.

Thus, AC = x + 5 = 15 + 5 cm = 20 cm

By using the Pythagoras theorem,

AB² + AC² = BC²

⇒ 15² + 20² = BC²

⇒ 225 + 400 = BC²

⇒ 625 = BC²

⇒ BC = $\sqrt{625}$

⇒ BC = 25

Hence, the sides of the triangle are 15 cm, 20 cm and 25 cm.